 VIE ET PHILOSOPHIE DE PYTHAGORE
VIE ET PHILOSOPHIE DE PYTHAGORE
Alors que Mnésarque, le père de Pythagore, se trouvait dans la ville de Delphes avec son épouse Parthenis, ils décidèrent de consulter l’oracle de Delphes pour savoir si les présages étaient favorables à leur voyage de retour en Syrie. Lorsque la Pythonisse (prophétesse d’Apollon) s’assit sur le trépied d’or au-dessus de l’orifice béant de l’oracle, elle ne répondit pas à la question posée mais annonça à Mnésarque que sa femme était enceinte et donnerait naissance à un fils était destiné à surpasser tous les hommes en beauté et en sagesse et que, tout au long de sa vie, il contribuerait au bien de l’humanité. Mnésarque fut tellement impressionné par la prophétie qu’il changea le nom de sa femme en Pythasis, en l’honneur de la prêtresse pythienne. Quand l’enfant naquit à Sidon en Phénicie, ce fut – comme l’avait dit l’oracle – un fils. Mnésarque et Pythasis nommèrent l’enfant Pythagoras, puisqu’il était prédestiné par l’oracle.
De nombreuses légendes étranges ont été conservées concernant la naissance de Pythagore. Certaines soutenaient qu’il n’était pas un homme mortel: il était l’un des dieux qui avaient pris un corps physique afin de venir au monde et d’instruire la race humaine. Pythagore était l’un des nombreux sages et sauveurs de l’Antiquité pour lesquels une conception immaculée est affirmée. Dans son Anacalypsis Godfrey Higgins écrit: « La première circonstance frappante qui relie l’histoire de Pythagore à celle de Jésus, est qu’ils étaient originaires du même pays, le premier étant né à Sidon, le second à Bethléem, les deux lieux se situant alors en Syrie. Le père de Pythagore, comme le père de Jésus, avaient été prophétiquement informé que son épouse devait donner naissance à un fils, qui deviendrait un bienfaiteur de l’humanité. Tous deux étaient nés lors d’un voyage, Marie et Pythasis, la mère de Pythagore, avaient un lien avec une entité, le Saint Esprit et Apollon (ou dieu Sol) qui apparut par la suite aux maris, et qui leur conseilla de n’avoir aucun rapport intime avec leur femme pendant leur grossesse. De par ces circonstances particulières, Pythagore était appelé comme Jésus, le fils de Dieu ; et était considéré comme étant sous l’influence de l’inspiration divine. «
Ce célèbre philosophe est né quelque part entre 600 et 590 avant JC, et la durée de sa vie a été estimée à près de cent ans.
Les enseignements de Pythagore indiquent qu’il connaissait parfaitement les préceptes de l’ésotérisme oriental et occidental. Il voyagea parmi les Juifs et fut instruit par les Rabbins des traditions secrètes de Moïse, le législateur d’Israël. Plus tard, l’École des Esséniens fut créée principalement dans le but d’interpréter les symboles pythagoriciens. Pythagore fut initié aux mystères égyptiens, babyloniens et chaldéens. Bien que certains pensent qu’il était un disciple de Zoroastre, il est douteux que son instructeur ait été l’Homme-Dieu révéré par les Parsis. Bien que les récits de ses voyages diffèrent, les historiens s’accordent à dire qu’il a visité de nombreux pays et étudié auprès de nombreux maîtres.
« Après avoir acquis tout ce qu’il lui fut possible d’apprendre des philosophes grecs et avoir été, vraisemblablement, initié aux mystères Eleusiniens, il se rendit en Égypte et, après plusieurs rebuffades et refus, il réussit finalement à être initié aux Mystères d’Isis, par les prêtres de Thèbes, puis cet intrépide «menuisier» se dirigea vers la Phénicie et la Syrie où les mystères d’Adonis lui furent révélés, traversa la vallée de l’Euphrate assez longtemps pour s’initier aux secrets des Chaldéens, qui habitaient encore dans les environs de Babylone. Puis il prit le chemin de la Médie et de la Perse, pour vivre sa plus grande aventure dans l’Hindoustan où il resta plusieurs années comme élève et initié des savants Brahmanes d’Ellora. » (Ancient Freemasonry, par Frank C. Higgins, 32 °.) Le même auteur ajoute que le nom de Pythagore est encore conservé dans les archives des brahmanes sous le nom de Yavancharya, le professeur ionien.
Pythagore aurait été le premier homme à se dire philosophe ; en fait, le monde lui doit le mot philosophe. Avant cette époque, les sages se nommaient eux-mêmes des sages, ce qui était interprété comme signifiant « ceux qui savent. » Pythagore, plus modeste, inventa le mot philosophe, qu’il définissait comme « celui qui tente de découvrir la sagesse. »
Au retour de ses errances, Pythagore fonda une école ou, comme on l’appelle parfois, une université à Crotone, une colonie dorienne du sud de l’Italie. À son arrivée dans cette cité, il fut regardé avec méfiance, mais peu de temps après, ceux qui occupaient des postes importants dans les colonies avoisinantes se mirent à rechercher ses conseils en matière de grandes décisions. Il rassembla autour de lui un petit groupe de disciples sincères qu’il instruisit dans la sagesse secrète qui lui avait été révélée, ainsi que dans les principes fondamentaux des mathématiques occultes, de la musique et de l’astronomie, qu’il considérait comme la base triangulaire de tous les arts et sciences.
À l’âge de soixante ans environ, il épousa l’une de ses disciples et sept enfants naquirent de cette union. Son épouse était une femme remarquable, qui non seulement l’inspira pendant toute sa vie mais qui, après son assassinat, continua à promulguer ses doctrines.
Comme c’est souvent le cas avec le génie, Pythagore, par son franc-parler, suscitait une hostilité à la fois politique et personnelle. Parmi ceux qui postulaient à l’initiation, il y en avait un qui, parce que Pythagore refusait de l’admettre, était déterminé à détruire l’homme et sa philosophie. Par la propagande mensongère, cet individu mécontent empoisonna l’esprit du peuple contre le philosophe. Sans avertissement, une bande de meurtriers incendia le petit groupe de bâtiments où le grand enseignant et ses disciples habitaient, et ainsi mourut Pythagore.
Les récits de la mort du philosophe diffèrent. Certains disent qu’il fut assassiné avec ses disciples; d’autres, qu’en fuyant Crotone avec un petit groupe de fidèles, il fût brûlé vif par ses ennemis dans une petite maison où le groupe avait décidé de se reposer pour la nuit. Un autre récit indique que, se trouvant pris au piège dans le bâtiment en feu, les disciples s’étaient jetés dans les flammes, faisant de leur propre corps un pont sur lequel Pythagore s’était échappé, pour ensuite mourir le cœur brisé après avoir constaté la stérilité apparente de ses efforts pour servir et éclairer l’humanité.
Ses disciples survivants ont tenté de perpétuer ses doctrines, mais ils ont été persécutés de toutes parts et il reste très peu de témoignages de la grandeur de ce philosophe aujourd’hui. Il est dit que les disciples de Pythagore ne s’adressaient jamais à lui en l’appelant par son propre nom, mais toujours le Maître ou cet homme.
Cela est peut-être dû au fait que le nom de Pythagore était censé être constitué d’un certain nombre de lettres spécialement agencées ayant une signification sacrée. Le magazine Word a publié un article de TR Prater montrant que Pythagore initiait ses adeptes au moyen d’une certaine formule dissimulée dans les lettres de son propre nom. Cela peut expliquer pourquoi le mot Pythagoras était si vénéré.
Après la mort du philosophe, son école se désintégra peu à peu, mais ceux qui avaient bénéficié de ses enseignements révéraient sa mémoire, car de son vivant, ils avaient respecté l’homme. Au fil du temps, Pythagore en vint à être considéré comme un dieu et ses disciples dispersés étaient liés par leur admiration commune pour le génie transcendant de leur professeur Edouard Schure, dans son Pythagoras and the Delphic Mysteries, rapporte l’incident suivant comme un exemple du lien de fraternité qui unissait les membres de l’école pythagoricienne:
« L’un d’entre eux, tomba malade et étant pauvre, il fut gentiment accueilli par un aubergiste. Avant de mourir, il traça quelques signes mystérieux (le pentagramme sans doute) sur la porte de l’auberge et dit à l’hôte inquiet : un de mes frères paiera mes dettes. Un an plus tard, alors qu’un étranger passait devant cette auberge, il vit les signes et dit à l’hôte: « Je suis pythagoricien, un de mes frères est mort ici, dites-moi ce que je vous dois pour lui. »
Frank C. Higgins, 32 °, présente un excellent recueil des principes de Pythagore dans les lignes suivantes: celle de « Mathematicus », assurant à ses élèves la maîtrise des mathématiques et de la géométrie, qui était alors, comme ce serait le cas maintenant, si la maçonnerie était correctement inculquée, la base sur laquelle toutes les autres connaissances étaient érigées. Deuxièmement, le degré de « Théorétique », qui traitait des applications superficielles des sciences exactes, et enfin le degré de « Electus », qui autorisait le candidat à passer à la lumière de la plus grande illumination qu’il était capable d’absorber. Les élèves de l’école pythagoricienne étaient divisés en « exoterici » ou élèves des classes supérieures et « esoterici » après avoir passé le troisième degré d’initiation et avoir eu accès à la sagesse secrète. Le silence, le secret et l’obéissance inconditionnelle étaient les principes cardinaux de ce grand ordre. (Ancient Freemasonry.)
FONDAMENTAUX PYTHAGORICIENS
L’étude de la géométrie, de la musique et de l’astronomie était considérée comme essentielle à une compréhension rationnelle de Dieu, de l’homme ou de la nature, et personne ne pouvait accompagner Pythagore en tant que disciple s’il n’était pas familiarisé avec ces sciences. Beaucoup se présentaient à son école. Chaque candidat était testé sur ces trois sujets et, s’il était trouvé ignorant, il était renvoyé sans préavis.
Pythagore n’était pas cependant pas un extrémiste. Il enseignait la modération en toutes choses plutôt que l’excès dans tout, car il croyait qu’un excès de vertu était en soi un vice. Une de ses déclarations préférées était: « Nous devons éviter avec le plus grand soin et amputer avec le feu et l’épée, et par tous les autres moyens, du corps la maladie; de l’âme l’ignorance; du ventre le luxe, d’une ville la sédition, de la famille la discorde et de toutes choses l’excès. » Pythagore croyait aussi qu’il n’y avait pas de crime égal à celui de l’anarchie.
« Tous les hommes savent ce qu’ils veulent, mais peu savent ce dont ils ont besoin. » Pythagore avertissait ses disciples que lorsqu’ils priaient, ils ne devaient pas prier pour eux-mêmes; que lorsqu’ils demandaient des choses aux dieux, ils ne devaient pas demander des choses pour eux-mêmes, car aucun homme ne sait ce qui est bon pour lui et c’est pour cette raison qu’il était inutile de demander des choses qui, si elles étaient obtenues, ne feraient que nuire.
Le Dieu de Pythagore était la Monade ou l’Un qui est Tout. Il a décrit Dieu comme le mental suprême distribué dans toutes les parties de l’univers – la cause de toutes les choses, l’intelligence de toutes choses et le pouvoir dans toutes choses. Il déclarait en outre que le mouvement de Dieu était circulaire, que le corps de Dieu était composé de la substance de la lumière et que la nature de Dieu se composait de la substance de la vérité.
Il affirmait que manger de la viande assombrissait les facultés de raisonnement. Bien qu’il ne condamna pas son utilisation ou ne s’en abstienne totalement, il disait que les juges devraient s’abstenir de manger de la viande avant un procès, afin que ceux qui comparaissaient devant eux pussent recevoir les décisions les plus honnêtes et justes. Lorsque Pythagore décida (comme il le faisait souvent) de se retirer dans le temple de Dieu pour une longue période de méditation et de prière, il emportait une réserve de nourriture et de boissons spécialement préparées. La nourriture consistait en des parties égales de graines de pavot et de sésame, de peau d’oignon de mer dont le jus avait été soigneusement extrait, de fleurs de jonquille, de feuilles de mauve et d’une pâte d’orge et de pois. Celles-ci se combinaient avec l’ajout de miel sauvage. En guise de boisson, il prenait des graines de concombres, des raisins secs (avec les graines enlevées), des fleurs de coriandre, des graines de mauve et de pourpier, du fromage, de la farine et de la crème, mélangés et sucrés avec du miel sauvage. Pythagore prétendait que c’était là le régime d’Héraclès lorsqu’il errait dans le désert libyen et qu’il avait été concocté selon la formule donnée à ce héros par la déesse Cérès elle-même.
La méthode de guérison préférée des pythagoriciens était le cataplasme. Ils connaissaient également les propriétés magiques d’un grand nombre de plantes. Pythagore appréciait les propriétés médicinales de l’oignon de mer et aurait écrit un volume entier sur le sujet. Cet ouvrage a disparu. Pythagore avait découvert que la musique avait un grand pouvoir thérapeutique et il préparait des harmonies spéciales pour diverses maladies.
Il avait apparemment expérimenté aussi la thérapie par la couleur, avec un certain succès. L’un de ses processus curatifs uniques résultait de sa découverte de la valeur curative de certains versets de l’Odyssée et de l’Iliade d’Homère. Il les faisait lire aux personnes souffrant de certaines maladies. Il s’opposait à la chirurgie sous toutes ses formes ainsi qu’à la cautérisation. Il ne permettait pas la défiguration du corps humain, car, à son avis, c’était un sacrilège contre la demeure des dieux.
Pythagore enseignait que l’amitié était la plus parfaite de toutes les relations. Il disait que dans la nature il y avait une amitié de tous pour tous; des dieux pour les hommes; des doctrines les unes pour les autres; de l’âme pour le corps; de la partie rationnelle pour la partie irrationnelle; de la philosophie pour la théorie; des hommes les uns pour les autres; des compatriotes les uns pour les autres; cette amitié existait aussi entre des étrangers, entre un homme et sa femme, ses enfants et ses serviteurs. Tous les liens sans amitié étaient des entraves et il n’y avait aucune vertu dans leur maintien. Pythagore croyait que les relations étaient essentiellement mentales plutôt que physiques et qu’un étranger d’intellect sympathique était plus proche de lui qu’une relation de sang dont le point de vue était en contradiction avec le sien. Il définissait la connaissance comme le fruit de l’accumulation mentale. Il pensait que cela serait obtenu de nombreuses manières, mais principalement par l’observation. La sagesse était la compréhension de la source ou de la cause de toutes choses, et cela ne pouvait être obtenu qu’en élevant l’intelligence au point où elle connaitrait intuitivement l’invisible se manifestant à l’extérieur par le visible et deviendrait ainsi capable de se mettre en rapport avec l’esprit des choses plutôt qu’avec leurs formes. La source ultime que la sagesse pourrait connaître était la Monade, le mystérieux atome permanent des Pythagoriciens.
Pythagore enseignait que l’homme et l’univers avaient été créés à l’image de Dieu; que les deux étant faites dans la même image, de la compréhension de l’un découlait la connaissance de l’autre. Il enseignait également qu’il y avait une interaction constante entre le macrocosme (l’univers) et le microcosme (le petit univers).
Il croyait que tous les corps sidéraux étaient vivants et que les planètes et les étoiles n’étaient que des corps renfermant des âmes, et des esprits de la même manière que la forme humaine visible n’est que le véhicule d’un organisme spirituel invisible, l’individu conscient. Pythagore considérait les planètes comme des divinités magnifiques, dignes de l’adoration et du respect de l’homme. Toutes ces divinités, cependant, étaient considérées comme subordonnées à la Première Cause Unique au sein de laquelle elles existaient toutes temporairement, étant donné que la mortalité existe au milieu de l’immortalité.
Le célèbre Y pythagoricien représentait le pouvoir du choix et était utilisé dans les Mystères comme emblème de la croisée des chemins. La tige centrale séparée en deux parties, l’une se ramifiant à droite et l’autre à gauche. La branche de droite s’appelait la Sagesse Divine et celle de gauche la Sagesse Terrestre. La jeunesse, personnifiée par le candidat, marchant sur le Chemin de la vie, symbolisé par la tige centrale du Υ, atteignait le point où le Chemin se divise.
Le néophyte devait alors choisir s’il emprunterait le chemin de gauche et, suivant les impératifs de sa nature inférieure, entamerait une période de folie et de manque de réflexion qui entraînerait inévitablement sa perte, ou s’il prendrait la voie de droite et par l’intégrité, le travail et la sincérité retrouverait finalement l’union avec les immortels dans les sphères supérieures. Il est probable que Pythagore avait obtenu son concept du Υ auprès des Égyptiens, qui incluaient dans certains de leurs rituels initiatiques une scène dans laquelle le candidat était confronté à deux figures féminines. L’une d’entre elles, voilée et vêtue de la robe blanche du temple, invitait le néophyte à entrer dans les salles d’apprentissage; l’autre, parée de bijoux, symbolisant les trésors terrestres et portant dans ses mains un plateau chargé de raisins (emblématique de la fausse lumière), cherchait à l’attirer dans les chambres de la dissipation. Ce symbole est toujours conservé sur les cartes de tarot, où il s’appelle La fourche des voies. Le bâton fourchu a été le symbole de la vie parmi de nombreuses nations et il a été placé dans le désert pour indiquer la présence d’eau.
En ce qui concerne la théorie de la transmigration diffusée par Pythagore, il existe des divergences d’opinion. Selon un point de vue, il enseignait que les mortels qui, au cours de leur existence terrestre, devenaient, par leurs actions, comme certains animaux, revenaient sur terre sous la forme des bêtes auxquelles ils ressemblaient. Ainsi, une personne timide reviendrait sous la forme d’un lapin ou d’un cerf; une personne cruelle sous la forme d’un loup ou d’un autre animal féroce; et une personne rusée sous les traits d’un renard. Ce concept, cependant, ne rentre pas dans le schéma général des enseignements de Pythagore et il est beaucoup plus probable qu’il ait été donné sous une forme allégorique plutôt que littérale. Il s’agissait de transmettre l’idée que les êtres humains deviennent bestiaux lorsqu’ils se laissent dominer par leurs propres désirs inférieurs et leurs tendances destructrices. Il est probable que le terme transmigration doit être compris comme ce qu’on appelle plus communément la réincarnation, doctrine que Pythagore a dû rencontrer directement ou indirectement en Inde et en Égypte. Le fait qu’il ait accepté la théorie des réapparitions successives de la nature spirituelle sous forme humaine se trouve dans une note de bas de page dans l’ histoire de la magie de Eliphas Levi : « Il était un champion important de ce qu’on appelait la doctrine de la métempsycose, comprise comme la transmigration de l’âme dans des corps successifs ; il avait été (a) Aethalides, un fils de Mercure, (b) Euphorbus, fils de Panthus, qui a péri aux mains de Ménélas dans la guerre de Troie, (c) Hermotimus, un prophète de Clazomenae, un ville d’Ionie, (d) un humble pêcheur et enfin (e) le philosophe de Samos.
Pythagore enseignait également que chaque espèce de créature avait ce qu’il a appelé un sceau, donné par Dieu, et que la forme physique de chacun était l’impression de ce sceau sur la cire de substance matérielle. Ainsi, chaque corps était empreint de la dignité de son modèle divinement donné. Pythagore croyait que finalement l’homme atteindrait un état où il se débarrasserait de sa nature et de sa fonction grossière dans un corps d’éther spiritualisé qui serait juxtaposé à sa forme physique à tout moment et qui pourrait être la huitième sphère, ou Antichtone. De là, il monterait au royaume des immortels, auquel il appartenait par droit divin.
Il enseignait que tout dans la nature était divisible en trois parties et que personne ne pouvait devenir vraiment sage qui ne considérait pas chaque problème comme étant triangulaire. Il disait : « Établissez le triangle et le problème est résolu aux deux tiers »; ainsi que, « toutes les choses consistent en trois ». En conformité avec ce point de vue, Pythagore divisait l’univers en trois parties, qu’il appelait le monde suprême, le monde supérieur et le monde inférieur. Le monde suprême, était une essence spirituelle subtile et interpénétrée qui imprégnait toutes les choses et, par conséquent, le véritable plan de la Déité Suprême elle-même, omniprésente, omnipotente et omnisciente. Les deux mondes inférieurs existaient dans la nature de cette sphère suprême. Le monde supérieur était la demeure des immortels. C’était aussi la demeure des archétypes ou des sceaux; leurs natures ne participaient en aucune manière du matériau de la terre, mais elles, ne jetant leur ombre que sur le fond (le monde inférieur), ne pouvaient être connues que par leurs ombres. Le troisième, ou monde inférieur, était la maison de ces créatures qui avaient une substance matérielle ou qui étaient engagées dans un travail avec ou sur une substance matérielle. Par conséquent, cette sphère était la maison des dieux mortels, les Demiurges, les anges qui travaillent avec les hommes; ainsi que les dæmons qui participent à la nature de la terre; et enfin l’humanité et les royaumes inférieurs, ceux temporairement de la terre mais capables de s’élever au-dessus de cette sphère par la raison et la philosophie.
Les chiffres 1 et 2 ne sont pas considérés comme des chiffres par les pythagoriciens, car ils caractérisent les deux sphères super-extraordinaires. Les nombres de Pythagore commencent donc par 3, le triangle et 4, le carré. Ceux-ci ajoutés au 1 et au 2, produisent le 10, le grand nombre de toutes choses, l’archétype de l’univers. Les trois mondes étaient appelés réceptacles. Le premier était le réceptacle des principes, le second était le réceptacle des intelligences et le troisième, ou le plus bas, était le réceptacle des quantités.
« Les solides symétriques étaient considérés par Pythagore et par les penseurs grecs après lui comme de la plus grande importance. Pour être parfaitement symétriques ou régulier, un solide doit avoir un nombre égal de faces se rejoignant à chacun de ses angles, et ces faces doivent être des polygones réguliers égaux, c’est-à-dire des figures dont les côtés et les angles sont tous égaux. Pythagore peut être crédité de la grande découverte qu’il n’y a que cinq solides de ce type.
« Or, les Grecs croyaient que le monde [l’univers matériel] était composé de quatre éléments – la terre, l’air, le feu, l’eau – et, dans l’esprit grec, la forme des particules des éléments était inévitablement celle des solides réguliers. Les particules de la Terre étaient cubiques, le cube étant le solide régulier ayant la plus grande stabilité; les particules de feu étaient tétraédriques, le tétraèdre étant le solide le plus simple et donc le plus léger. Les particules d’eau étaient icosaédriques pour la raison inverse, tandis que les particules d’air, intermédiaires entre les deux, étaient octaédriques. Le dodécaèdre était, pour ces anciens mathématiciens, le plus mystérieux des solides; c’était de loin le plus difficile à construire, le dessin précis du pentagone régulier nécessitant une application assez élaborée du grand théorème de Pythagore. D’où la conclusion, comme le dit Platon, que « ceci (le dodécaèdre régulier) est la déité employée pour tracer le plan de l’univers ». (H. Stanley Redgrove, Bygone Beliefs.)
- Redgrove n’a pas mentionné le cinquième élément des anciens Mystères, celui qui complèterait l’analogie entre les solides symétriques et les éléments. Ce cinquième élément, ou éther, était appelé par les Hindous akasa. Il était étroitement corrélé à l’éther hypothétique de la science moderne et constituait la substance interpénétrée imprégnant tous les autres éléments et agissant comme un solvant et un dénominateur communs. Le solide à douze faces se référait aussi subtilement aux Douze Immortels qui étaient apparus dans l’univers et aux douze circonvolutions du cerveau humain – les véhicules de ces Immortels dans la nature de l’homme. Tandis que Pythagore, conformément aux autres hommes de son époque, pratiquait la divination (possiblement l’arithmomancie), il n’y a pas d’informations précises sur les méthodes qu’il utilisait. Il aurait possédé une roue remarquable au moyen de laquelle il pouvait prédire des événements futurs et avait appris l’hydromancie des Égyptiens. Il croyait que le laiton avait des pouvoirs oraculaires, car même quand tout était parfaitement immobile, il y avait toujours une vibration dans les bols de cuivre. Adressant un jour une prière à l’esprit d’une rivière, une voix sortit de l’eau et dit : « Pythagore, je te salue. » On lui prêtait le pouvoir de faire entrer les Dæmons dans l’eau et de perturber ainsi la surface, des prédictions étaient faites en interprétant ces agitations.
Après avoir bu de l’eau un jour de printemps, l’un des Maîtres de Pythagore annonça que l’esprit de l’eau venait de prédire qu’un grand tremblement de terre se produirait le lendemain, une prophétie qui s’accomplit effectivement. Il est fort probable que Pythagore possédait un pouvoir hypnotique, non seulement sur l’homme, mais aussi sur les animaux. Il pouvait amener un oiseau à changer le cours de son vol, un ours à cesser ses ravages sur une communauté et un taureau à changer son régime alimentaire, en exerçant une influence mentale. Il était également doué pour la seconde vue, étant capable de voir les choses à distance et de décrire avec précision des incidents qui ne s’étaient pas encore produits.
LES APHORISMES SYMBOLIQUES DE PYTHAGORE
Jamblique a rassemblé trente-neuf des paroles symboliques de Pythagore et les a interprétées. Celles-ci ont été traduites du grec par Thomas Taylor. La déclaration aphoristique était l’une des méthodes d’enseignement préférées de l’université pythagoricienne de Crotone. Dix des plus représentatifs de ces aphorismes sont reproduits ci-dessous avec une brève interprétation de leurs significations cachées.
- Déclin des voies publiques, marchez sur des chemins peu fréquentés. Il faut comprendre que ceux qui désirent la sagesse doivent la chercher dans la solitude.
- Gouvernez votre langue avant toute autre chose, en suivant les dieux. Cet aphorisme avertit l’homme que ses paroles, au lieu de le représenter, le déforment et que, dans le doute, il devrait toujours se taire.
III. Le vent qui souffle, adore le son. Pythagore rappelle ici à ses disciples que les décrets de Dieu sont entendu dans la voix des éléments et que toutes les choses de la nature se manifestent par l’harmonie, le rythme, l’ordre qui sont les attributs de la divinité.
- Aide un homme à lever un fardeau; mais ne l’aide pas à le poser. L’élève est chargé d’aider le diligent mais jamais d’aider ceux qui cherchent à se soustraire à leurs responsabilités, car c’est un grand péché que d’encourager l’indolence.
- Ne parlez pas des préoccupations de Pythagore sans lumière. Le monde est averti ici qu’il ne devrait pas tenter d’interpréter les mystères de Dieu et les secrets des sciences sans illumination spirituelle et intellectuelle.
- Ayant quitté votre maison, ne vous retournez pas, car les furies seront vos servantes. Pythagore avertit ici ses partisans que ceux qui commencent la recherche de la vérité et, après avoir appris une partie du mystère, se découragent et tentent de retourner à leurs anciennes habitudes de vice et d’ignorance, souffriront énormément; car il vaut mieux ne rien savoir de la Divinité que d’apprendre un peu puis s’arrêter sans tout apprendre.
VII. Nourrissez un coq, mais ne le sacrifiez pas; car il est sacré pour le soleil et la lune. Deux grandes leçons sont dissimulées dans cet aphorisme. Le premier est un avertissement contre le sacrifice des êtres vivants aux dieux, car la vie est sacrée et l’homme ne devrait pas la détruire même en offrande à la divinité. La seconde avertit l’homme que le corps humain, appelé ici coq, est sacré pour le soleil (Dieu) et la lune (Nature) et devrait être gardé et préservé comme le moyen d’expression le plus précieux de l’homme. Pythagore a également mis en garde ses disciples contre le suicide.
VIII. Ne recevez pas une hirondelle dans votre maison. Cela avertit le chercheur de la vérité de ne pas laisser entrer dans sa vie des pensées confuses, ni des personnes instables. Il doit toujours s’entourer de penseurs inspirés rationnellement et de travailleurs consciencieux.
- N’offrez pas facilement votre main droite à quiconque. Cela avertit le disciple de garder ses propres conseils et de ne pas offrir la sagesse et la connaissance (sa main droite) à ceux qui sont incapables de les apprécier. La main représente ici la vérité, qui relève ceux qui sont tombés à cause de l’ignorance; mais comme beaucoup de non-initiés ne désirent pas la sagesse, ils couperont la main qui leur est tendue. Seul le temps peut amener la rédemption des masses ignorantes
- En quittant votre couche, roulez-les ensemble et effacez l’impression du corps. Pythagore incite ses disciples qui s’étaient réveillés du sommeil de l’ignorance dans l’état d’intelligence éveillé à éliminer de leur esprit tout souvenir de leurs anciennes ténèbres spirituelles; car un homme sage en passant ne laisse aucune forme derrière lui, que les autres moins intelligents, la voyant, utiliseront comme moule pour créer des idoles.
Les plus célèbres des fragments de Pythagore sont les Vers d’or, attribués à Pythagore lui-même, mais sa paternité est douteuse. Les vers d’or contiennent un bref résumé de tout le système de philosophie qui constitue la base des doctrines éducatives de Crotone ou, comme on l’appelle plus communément, l’école italique. Ces versets s’ouvrent en conseillant au lecteur d’aimer Dieu, de vénérer les grands héros et de respecter les élémentaux. Ils pressent alors l’homme de penser avec soin à sa vie quotidienne et de préférer les trésors de l’esprit et de l’âme aux accumulations de biens terrestres. Les versets promettent aussi à l’homme que s’il se lève au-dessus de sa nature matérielle inférieure et cultive le contrôle de soi, il sera finalement acceptable aux yeux des dieux, sera réuni avec eux et participera à leur immortalité. (Il est assez significatif de noter que Platon a payé un grand prix pour certains manuscrits de Pythagore qui avaient été sauvés lors de la destruction de Crotone. (Historia Deorum Fatidicorum, Genève, 1675.)
ASTRONOMIE PYTHAGORICIENNE
Selon Pythagore, la position de chaque corps dans l’univers était déterminée par la dignité essentielle de ce corps. Le concept populaire de son époque était que la terre occupait le centre du système solaire; que les planètes, y compris le soleil et la lune, tournaient autour de la terre; et que la terre elle-même était plate et carrée. Contrairement à ce concept, et indépendamment des critiques, Pythagore a déclaré que le feu était le plus important de tous les éléments; que le centre était la partie la plus importante de chaque corps; et que, tout comme le feu de Vesta était au milieu de chaque foyer, au milieu de l’univers se trouvait une sphère enflammée de rayonnement céleste. Ce globe central était appelé la Tour de Jupiter, le Globe de l’Unité, la Grande Monade et l’Autel de Vesta. Comme le nombre sacré 10 symbolisait la somme de toutes les parties et la complétude de toutes choses, il était naturel que Pythagore divise l’univers en dix sphères, symbolisées par dix cercles concentriques. Ces cercles commençaient au centre avec le globe du feu divin; puis les sept planètes, la terre et une autre planète mystérieuse appelée Antichthon, qui n’était jamais visible. Les opinions diffèrent quant à la nature d’Antichthon. Clément d’Alexandrie croyait qu’elle représentait la masse du ciel; d’autres étaient d’avis que c’était la lune. Plus probablement, il s’agissait de la huitième sphère mystérieuse des anciens, la planète sombre qui se déplaçait sur la même orbite que la terre, mais qui était toujours cachée de la terre par le corps du soleil, étant exactement en opposition avec la terre. Etait-ce la mystérieuse Lilith à propos de laquelle les astrologues ont spéculé si longtemps?
Isaac Myer a déclaré: « Les pythagoriciens ont soutenu que chaque étoile était un monde ayant sa propre atmosphère, avec une immense étendue qui l’entourait : l’éther. » (La Qabbalah.) Les disciples de Pythagore ont également vénéré la planète Vénus, car c’était la seule planète assez brillante pour jeter une ombre. Comme étoile du matin, Vénus est visible avant le lever du soleil et, comme étoile du soir, elle brille immédiatement après le coucher du soleil. De par ces qualités, un certain nombre de noms lui ont été donnés par les anciens. Étant visible dans le ciel au coucher du soleil, elle s’appelait vesper, et comme elle se levait avant le soleil, elle s’appelait la fausse lumière, l’étoile du matin, ou Lucifer, qui signifie le porteur de lumière. À cause de cette relation avec le soleil, la planète était aussi appelée Vénus, Astarté, Aphrodite, Isis et La Mère des Dieux. Il est possible qu’à certaines saisons de l’année et sous certaines latitudes, Vénus ait été un croissant détecté sans l’aide d’un télescope. Cela expliquerait le croissant que l’on voit souvent en relation avec les déesses de l’antiquité, dont les histoires ne correspondent pas aux phases de la lune. La connaissance exacte que Pythagore possédait au sujet de l’astronomie avait sans doute été acquise dans les temples égyptiens, car ses prêtres comprenaient la véritable relation des corps célestes plusieurs milliers d’années avant que cette connaissance ne soit révélée au monde non initié. Le fait que les connaissances acquises dans les temples lui aient permis de faire des affirmations nécessitant deux mille ans pour être vérifiées prouve pourquoi Platon et Aristote ont tant apprécié la profondeur des anciens Mystères. Au milieu de l’ignorance scientifique générale et sans l’aide d’instruments modernes, les prêtres-philosophes avaient découvert les véritables principes fondamentaux de la dynamique universelle.
Une application intéressante de la doctrine pythagoricienne des solides géométriques exposée par Platon se trouve dans The Canon. « Presque tous les vieux philosophes, dit son auteur anonyme, ont conçu une théorie harmonique à l’égard de l’univers et la pratique a continué jusqu’à ce que l’ancien monde de la philosophie se soit éteint. Kepler (1596), pour démontrer la doctrine platonicienne selon laquelle l’univers était formé des cinq solides réguliers, a proposé la règle suivante: « La terre est un cercle, le mesureur de tous. Elle décrit un dodécaèdre; le cercle comprenant ceci sera Mars. Mars décrit un tétraèdre; la sphère y compris Jupiter. Décrivez un cube autour de Jupiter, la sphère qui le contient sera Saturne. Maintenant, inscrivez dans la terre un icosaèdre; le cercle qui y sera inscrit sera Vénus. Inscrivez un octaèdre dans Vénus; le cercle qui y est inscrit sera Mercure » (Mysterium Cosmographicum, 1596). Cette règle ne peut pas être prise au sérieux en tant que véritable énoncé des proportions du cosmos, de plus, elle ne ressemble pas vraiment aux rapports publiés par Copernic au début du seizième siècle.
Pourtant, Kepler était très fier de sa formule et disait qu’il la valorisait plus que l’électorat de Saxe. Il a également été approuvé par les deux autorités éminentes, Tycho et Galilée, qui l’ont bien compris. Kepler lui-même ne donne jamais le moindre indice sur la manière d’interpréter sa précieuse règle. « L’astronomie platonicienne ne s’intéressait pas à la constitution matérielle ou à la disposition des corps célestes, mais considérait les étoiles et les corps célestes principalement comme points focaux de l’intelligence Divine. L’astronomie physique était considérée comme la science des « ombres », l’astronomie philosophique comme la science des « réalités ».
MATHEMATIQUES PYTHAGORICIENNES
En ce qui concerne la signification secrète des nombres, beaucoup de spéculations ont été émises. Bien que de nombreuses découvertes intéressantes aient été faites, on peut dire avec certitude qu’avec la mort de Pythagore, la clé de cette science a été perdue. Pendant près de 2500 ans, les philosophes de toutes les nations ont tenté de démêler l’écheveau de Pythagore, mais apparemment aucun n’a abouti. Malgré les tentatives faites pour effacer toutes les traces des enseignements de Pythagore, des fragments subsistent qui donnent des indices sur certaines des parties les plus simples de sa philosophie. Les principaux secrets n’ont jamais été écrits, mais ont été communiqués oralement à quelques disciples choisis. Ceux-ci apparemment ne divulguèrent pas leurs secrets aux profanes, le résultat étant que, lorsque la mort a scellé leurs lèvres, les arcanes sont morts avec eux.
Certaines des écoles secrètes dans le monde d’aujourd’hui sont des perpétuations des anciens mystères et, bien qu’il soit fort possible qu’ils possèdent certaines des formules numériques originales, il n’y a aucune preuve de cela dans les volumineux écrits qui en ont été issus ces cinq cents dernières années. Bien que mentionnant fréquemment Pythagore, ces écrits ne montrent aucun signe d’une connaissance plus complète de ses doctrines complexes que les spéculateurs grecs post-pythagoriciens, qui parlaient beaucoup, écrivaient peu, savaient encore moins et dissimulaient leur ignorance sous une série de mystérieuses allusions et promesses. Ici et là, parmi les produits littéraires des premiers écrivains, on trouve des énoncés énigmatiques qu’ils ne font aucun effort d’interpréter. L’exemple suivant est cité par Plutarque :
« Les pythagoriciens ont donné aux nombres et aux figures géométriques les dénominations des dieux. Le triangle équilatéral est appelé Minerve, née de la tête de Jupiter, et Tritogénie, parce que ce triangle peut être divisé également par trois perpendiculaires tirées de ses trois angles. L’unité est Apollon, parce qu’elle est le symbole de la persuasion et de la candeur ; la dyade a les noms de discorde et d’audace, et le nombre trois, celui de justice ; car entre l’injustice commise et l’injustice reçue, qui sont les deux excès opposés, la Justice tient le milieu et établit l’égalité. Le quaternaire, ce nombre mystérieux formé des trente-six unités, et qui, comme on sait, est leur serment le plus sacré, porte le nom de kosmos (monde): il est composé des quatre premiers nombres pairs et des quatre premiers impairs adoptés ensemble. » (Isis et Osiris.)
Plus tôt dans le même ouvrage, Plutarque notait également: « …le triangle exprime la puissance de Pluton, de Bacchus et de Mars; le carré, celle de Rhéa, de Vénus, de Cérès, de Vesta et de Junon; le dodécagone, celle de Jupiter, et la figure à 56 angles, celle de Typhon, comme l’enseigne Eudoxe. » Plutarque ne prétend pas expliquer la signification intérieure des symboles, mais croit que la relation établie par Pythagore entre les solides géométriques et les dieux était le résultat d’images que le grand sage a vues dans les temples égyptiens.
Albert Pike, le grand symboliste maçonnique, a admis qu’il y avait de nombreux points sur lesquels il ne pouvait obtenir aucune information fiable. Dans son Symbolism, pour les 32 ° et 33 °, il écrivait: « Je ne comprends pas pourquoi le 7 devrait s’appeler Minerve, ou le cube, Neptune. » Plus loin, il ajoutait: « Sans aucun doute, les noms donnés par les pythagoriciens aux différents numéros étaient eux-mêmes énigmatiques et symboliques – et il est peu de doute qu’à l’époque de Plutarque, les significations cachées de ces noms avaient été perdues. Pythagore avait trop bien réussi à dissimuler ses symboles d’un voile impénétrable, sans explication orale. » Cette incertitude partagée par tous les vrais étudiants en la matière prouve de manière concluante qu’il n’est pas sage de formuler des affirmations définitives fondées sur les informations indéfinies et fragmentaires disponibles concernant le système pythagoricien de philosophie mathématique. Ce qui suit représente un effort pour rassembler quelques points saillants des archives éparses conservées par les disciples de Pythagore et d’autres personnes qui ont depuis approché sa philosophie.
METHODE DE SECURISATION DE LA PUISSANCE NUMERIQUE DES MOTS
La première étape pour obtenir la valeur numérique d’un mot consiste à le redéfinir dans sa langue d’origine. Cette méthode permet d’analyser avec succès des mots dérivés du grec ou de l’hébreu. Tous les mots doivent être épelés sous leur forme la plus ancienne et la plus complète. Les mots et les noms de l’Ancien Testament doivent donc être traduits dans les premiers caractères hébreux et les mots du Nouveau Testament dans le grec. Deux exemples aideront à clarifier ce principe.
Le Demiurge des Juifs est appelé en anglais Jéhovah, mais pour rechercher la valeur numérique du nom Jéhovah, il est nécessaire de résoudre le nom en lettres hébraïques. Il devient יהוה et se lit de droite à gauche. Les lettres hébraïques sont: ה, He; ו, Vau; ה, il; י, Yod; et quand inversé dans l’ordre anglais de gauche à droite, lire: Youd-He-Vau-He. En consultant le tableau suivant (image 5) des valeurs des lettres, on constate que les quatre caractères de ce nom sacré ont la signification numérique suivante: Yod est égal à 10. Il est égal à 5, Vau est égal à 6 et le second He est égal à 5. Par conséquent, 10 + 5 + 6 + 5 = 26, synonyme de Jéhovah. Si les lettres anglaises étaient utilisées, la réponse ne serait évidemment pas correcte.
Le deuxième exemple est le mystérieux panthéos gnostique Abraxas. Pour ce nom, la table grecque est utilisée. Abraxas en grec est Ἀβραξας. Α = 1, β = 2, ρ = 100, α = 1, ξ = 60, α = 1, ς = 200, la somme étant 365, le nombre de jours de l’année.
Ce numéro fournit la clé du mystère d’Abraxas, qui est le symbole des 365 éons, ou Esprits des Jours, rassemblés dans une personnalité composite. Abraxas est le symbole de cinq créatures et, comme le cercle de l’année est en réalité composé de 360 degrés, chacune des divinités émanantes représente un cinquième de cette puissance, ou 72, l’un des nombres les plus sacrés de l’Ancien Testament des Juifs dans leur système Qabbalistique. Cette même méthode est utilisée pour trouver la valeur numérique des noms des dieux et des déesses des Grecs et des Juifs.
Tous les nombres plus élevés peuvent être réduits à l’un des dix chiffres originaux et le 10 lui-même à 1. Par conséquent, tous les groupes de nombres résultant de la traduction des noms de divinités en leurs équivalents numériques ont une base dans l’un des dix premiers chiffres. Selon ce système, dans lequel les chiffres sont additionnés, 666 devient 6 + 6 + 6 ou 18, et celui-ci, à son tour, devient 1 + 8 ou 9. Selon Apocalypse, 144 000 doivent être sauvegardés. Ce nombre devient 1 + 4 + 4 + 0 + 0 + 0, ce qui équivaut à 9, prouvant ainsi que la Bête de Babylone et le numéro du sauvé se rapportent à l’homme lui-même, dont le symbole est le nombre 9. Ce système peut être utilisé avec succès avec les deux lettres grecques et hébraïques. Le système pythagoricien original de philosophie numérique ne contient aucun élément qui justifie la pratique actuellement en vogue qui consiste à changer le prénom ou le nom de famille dans l’espoir d’améliorer le tempérament ou la situation financière en modifiant les vibrations du nom.
Il existe également un système de calcul en vogue pour la langue anglaise, mais son exactitude fait l’objet d’un litige légitime. Il est comparativement moderne et n’a aucun lien avec le système hébraïque Qabbalistique ni avec la procédure grecque.
L’affirmation de certains selon laquelle il s’agit d’une méthode de Pythagore n’est étayée par aucune preuve tangible, et il existe de nombreuses raisons pour lesquelles une telle affirmation est intenable. Le fait que Pythagore ait utilisé 10 comme base de calcul, alors que ce système utilise 9 – un nombre imparfait – est en soi presque concluant. De plus, la disposition des lettres grecques et hébraïques ne correspond pas suffisamment à l’anglais pour permettre l’application des séquences numériques d’une langue aux séquences numériques d’une autre. Voir exemple ci-dessus.
INTRODUCTION A LA THEORIE PYTHAGORICIENNE DES NOMBRES
(L’esquisse suivante des mathématiques pythagoriciennes est une paraphrase des premiers chapitres de Theoretic Arithmetic de Thomas Taylor, la compilation la plus rare et la plus importante de fragments mathématiques existants de Pythagore.)
Les pythagoriciens considéraient que l’arithmétique était la mère des sciences mathématiques. Ceci est prouvé par le fait que la géométrie, la musique et l’astronomie en dépendent, mais ne lui sont pas supérieurs. Ainsi, la géométrie peut être supprimée mais l’arithmétique restera; mais si l’arithmétique est supprimée, la géométrie est éliminée. De la même manière, la musique dépend de l’arithmétique, mais l’élimination de la musique n’affecte l’arithmétique qu’en limitant l’une de ses expressions. Les Pythagoriciens ont également démontré que l’arithmétique était antérieure à l’astronomie, car cette dernière dépend à la fois de la géométrie et de la musique. La taille, la forme et le mouvement des corps célestes sont déterminés par l’utilisation de la géométrie. Leur harmonie et leur rythme par l’utilisation de la musique. Si l’astronomie est supprimée, ni la géométrie ni la musique ne sont impactées; mais si la géométrie et la musique sont éliminées, l’astronomie est détruite. La primauté de la géométrie et de la musique en astronomie est donc établie. L’arithmétique, cependant, est avant tout; elle est primaire et fondamentale.
Pythagore enseignait à ses disciples que la science des mathématiques est divisée en deux parties principales. La première concerne la multitude ou les éléments constitutifs d’une chose et la seconde la magnitude, la taille ou la densité relative d’une chose.
La magnitude est divisée en deux parties – la magnitude qui est stationnaire et la magnitude qui est mobile, le stationnaire étant prioritaire. La multitude est également divisée en deux parties, car elle est liée à elle-même et à d’autres choses, la première relation étant prioritaire. Pythagore a attribué la science de l’arithmétique à la multitude liée à elle-même, et l’art de la musique à la multitude liée à d’autres choses. De même, la géométrie était affectée à la magnitude stationnaire et les sphériques (utilisées en partie dans le sens de l’astronomie) à la magnitude mobile. La multitude et la magnitude étaient toutes deux circonscrites par la circonférence de l’esprit. La théorie atomique a démontré que la taille résultait du nombre, car une masse est composée d’unités minuscules, mais confondues avec celles qui ne le sont pas comme une seule substance simple.
En raison de la fragmentation des archives pythagoriciennes existantes, il est difficile d’arriver à une définition exacte des termes. Avant qu’il soit possible, cependant, de développer davantage le sujet, il est nécessaire d’éclairer le sens des mots nombre, monade et un.
La monade signifie (a) le UN tout compris. Les pythagoriciens ont appelé la monade « le nombre noble, le père des dieux et des hommes ». La monade signifie également (b) la somme de toute combinaison de nombres considérée dans son ensemble. Ainsi, l’univers est considéré comme une monade, mais les parties individuelles de l’univers (telles que les planètes et les éléments) sont des monades par rapport aux parties qui les composent elles-mêmes, bien qu’elles fassent à leur tour partie d’une plus grande monade formée de leur somme. La monade peut aussi être assimilée (c) à la graine d’un arbre qui, quand il est devenu grand, a beaucoup de branches (les nombres). En d’autres termes, les nombres sont à la monade ce que les branches de l’arbre sont à la graine de l’arbre. De l’étude de la mystérieuse monade de Pythagore, Leibnitz a développé sa magnifique théorie des atomes du monde – une théorie en parfait accord avec les anciens enseignements des Mystères, car Leibnitz lui-même était l’initiateur d’une école secrète. Par certains pythagoriciens, la monade est également considérée (d) comme synonyme de un.
Le nombre est le terme appliqué à tous les chiffres et leurs combinaisons. (Une interprétation stricte du terme nombre par certains pythagoriciens exclut 1 et 2.) Pythagore définit le nombre comme étant l’extension et l’énergie des éléments spermatiques contenues dans la monade. Les adeptes d’Hippase considéraient que le numéro était le premier modèle utilisé par les Démiurges dans la formation de l’univers. Celui- ci était défini par les platoniciens comme « le sommet du plus grand nombre ». Le premier diffère de la monade en ce que le terme monade est utilisé pour désigner la somme des parties considérées comme une unité, tandis que le premier est le terme appliqué à chacune de ses parties intégrales.
Il y a deux ordres de nombre: impair et pair. Parce que l’unité, ou 1, reste toujours indivisible, le nombre impair ne peut pas être divisé également. Ainsi, 9 est 4 + 1 + 4, l’unité au centre étant indivisible. De plus, si un nombre impair est divisé en deux parties, une partie sera toujours impaire et l’autre paire. Ainsi, 9 peut être 5 + 4, 3 + 6, 7 + 2 ou 8 + 1. Les Pythagoriciens considéraient que le nombre impair – dont la monade était le prototype – était défini et masculin. Cependant, ils n’étaient pas tous d’accord sur la nature de l’unité, ou 1. Certains l’ont déclarée positive, car si elle est ajoutée à un nombre pair (négatif), elle produit un nombre impair (positif). D’autres ont démontré que si l’unité est ajoutée à un nombre impair, celui-ci devient pair, rendant ainsi le masculin féminin. L’unité, ou 1, était donc considérée comme un nombre androgyne, prenant à la fois les attributs masculin et féminin; par conséquent à la fois impair et pair. Pour cette raison, les pythagoriciens l’appelèrent uniformément-étrange. Les pythagoriciens avaient coutume d’offrir des sacrifices d’un nombre inégal d’objets aux dieux supérieurs, tandis qu’un nombre pair était proposé aux déesses et aux esprits souterrains.
Tout nombre pair peut être divisé en deux parties égales, qui sont toujours soit impaires, soit paires. Ainsi, 10 par division égale donne 5 + 5, les deux nombres impairs. Le même principe est valable si les 10 sont divisés de manière inégale. Par exemple, dans 6 + 4, les deux parties sont paires; dans 7 + 3, les deux parties sont impaires; en 8 + 2, les deux parties sont à nouveau paires; et dans 9 + 1, les deux parties sont encore impaires. Ainsi, dans le nombre pair, quelle que soit la division, les parties seront toujours à la fois impaires ou paires. Les Pythagoriciens considéraient le nombre pair – dont la duade était le prototype – indéfini et féminin.
Les nombres impairs sont divisés par un dispositif mathématique – appelé « le tamis d’Ératosthène » – en trois classes générales: incomposite, composite et incomposite-composite.
Les nombres incomposite sont ceux qui n’ont pas de diviseur autre qu’eux-mêmes et une unité, tels que 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, etc. Par exemple, 7 n’est divisible que par 7, ce qui entre en soi une fois, et l’unité, qui entre 7 fois.
Les nombres composés sont ceux qui sont divisibles non seulement par eux-mêmes et par l’unité, mais aussi par un autre nombre, tel que 9, 15, 21, 25, 27, 33, 39, 45, 51, 57, etc. Par exemple, 21 est divisible non seulement par elle-même et par l’unité, mais aussi par 3 et par 7.
Les nombres composite-incomposite sont ceux qui n’ont pas de diviseur commun, bien que chacun d’eux soit capable de division, comme 9 et 25. Par exemple, 9 est divisible par 3 et 25 par 5, mais ni l’un ni l’autre n’est divisible par le diviseur de l’autre; ils n’ont donc pas de diviseur commun. Parce qu’ils ont des diviseurs individuels, ils sont appelés composites; et parce qu’ils n’ont pas de diviseur commun, ils sont appelés composites. En conséquence, le terme incomposite-composite a été créé pour décrire leurs propriétés. Les nombres pairs sont divisés en trois classes: égales, égales et étranges. Les uniformément-même les nombres sont tous dans un rapport binaire à partir de l’unité; ainsi: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512 et 1 024. La preuve du nombre pair-égal parfait est qu’il peut être divisé par deux et que les moitiés redeviennent également divisées par deux, à savoir 1/2 sur 64 = 32; 1/2 sur 32 = 16; 1/2 sur 16 = 8; 1/2 sur 8 = 4; 1/2 sur 4 = 2; 1/2 de 2 = 1; au-delà de l’unité, il est impossible d’aller.
Les uniformément-mêmes nombres possèdent certaines propriétés uniques. La somme de tout nombre de termes, mais le dernier terme est toujours égal au dernier terme moins un. Par exemple: la somme des premier et deuxième termes (1 + 2) est égale au troisième terme (4) moins un; ou, la somme des premier, deuxième, troisième et quatrième termes (1 + 2 + 4 + 8) est égale au cinquième terme (16) moins un.
Dans une série de façon-égale-même nombre, la première multipliée par la dernière est égale à la dernière, la deuxième multiplié par le deuxième à partir de la dernière est égale à la dernière, et ainsi de suite jusqu’à ce que dans une série impaire d’un nombre reste, ce qui multiplié par lui-même est égal au dernier numéro de la série; ou, dans une série paire, il reste deux nombres qui, multipliés l’un par l’autre, donnent le dernier numéro de la série. Par exemple: 1, 2, 4, 8, 16 est une série impaire. Le premier nombre (1) multiplié par le dernier nombre (16) est égal au dernier nombre (16). Le deuxième nombre (2) multiplié par le deuxième à partir du dernier nombre (8) est égal au dernier nombre (16). Étant une série impaire, le 4 est laissé au centre, et cela multiplié par lui-même est égal au dernier nombre (16).
Les nombres pairs-impairs sont ceux qui, lorsqu’ils sont divisés par deux, ne peuvent plus être divisés par deux. Ils sont formés en prenant les nombres impairs dans l’ordre séquentiel et en les multipliant par 2. Par ce processus, les nombres impairs 1, 3, 5, 7, 9, 11 produisent les nombres pairs-impairs 2, 6, 10, 14, 18. 22. Ainsi, un nombre sur quatre est pair-impair. Chacun des nombres pairs-impairs peut être divisé une fois, en 2, qui devient deux 1 et ne peut plus être divisé; ou 6, qui devient deux 3 et ne peut plus être divisé.
Une autre particularité des nombres pairs-impairs est que si le diviseur est impair, le quotient est toujours pair et si le diviseur est pair, le quotient est toujours impair. Par exemple: si 18 est divisé par 2 (un diviseur pair), le quotient est 9 (un nombre impair); si 18 est divisé par 3 (un diviseur impair), le quotient est 6 (un nombre pair).
Les nombres pairs-impairs sont également remarquables en ce que chaque terme correspond à la moitié de la somme des termes de chaque côté. Par exemple:
10 est la moitié de la somme de 6 et 14; 18 est la moitié de la somme de 14 et 22; et 6 est la moitié de la somme de 2 et 10.
Les chiffres étrangement bizarres ou inégaux sont un compromis entre les nombres pairs et les nombres pairs. Contrairement aux égaux, ils ne peuvent être réduits de moitié à l’unité; et contrairement à ce qui est normal, ils sont capables de plus d’une division en deux. Les nombres étrangement impairs sont formés en multipliant les nombres pairs supérieurs à 2 par les nombres impairs supérieurs à un. Les nombres impairs au-dessus de l’un sont 3, 5, 7, 9, 11, etc. Les nombres pairs supérieurs à 2 sont 4, 8, 16, 32, 64 et bientôt. Le premier nombre impair de la série (3) multiplié par 4 (le premier nombre pair-pair de la série) donne 12, le premier nombre impair.
En multipliant 5, 7, 9, 11, etc., par 4, on trouve des nombres étrangement impairs. Les autres nombres étrangement impairs sont produits en multipliant 3, 5, 7, 9, 11, etc., à leur tour, par les autres nombres pairs (8, 16, 32, 64, etc.). Un exemple de la réduction de moitié du nombre impair-impair est le suivant: 1/2 sur 12 = 6; 1/2 sur 6 = 3, ce qui ne peut être réduit de moitié, car les pythagoriciens ne divisaient pas l’unité.
Les nombres pairs sont également divisés en trois autres classes: super – parfait, faible et parfait.
Les nombres super – parfaits ou surabondants sont tels que la somme de leur fraction est supérieure à eux-mêmes. Par exemple: 1/2 sur 24 = 12; 1/4 = 6; 1/3 = 8; 1/6 = 4; 1/12 = 2; et 1/24 = 1. La somme de ces parties (12 + 6 + 8 + 4 + 2 + 1) est 33, ce qui est supérieur à 24, le nombre initial.
Les nombres faibles sont tels qu’ils ont la somme de leurs fractions inférieures à eux-mêmes. Par exemple: 1/2 sur 14 = 7; 1/7 = 2; et 1/14 = 1. La somme de ces parties (7 + 2 + 1) est 10, ce qui est inférieur à 14, le nombre d’origine.
Les nombres parfaits sont tels que la somme de leurs fractions égales à elles-mêmes. Par exemple: 1/2 sur 28 = 14; 1/4 = 7; 1/7 = 4; 1/14 = 2; et 1/28 = 1. La somme de ces parties (14 + 7 + 4 + 2 + 1) est égale à 28.
Les nombres parfaits sont extrêmement rares. Il n’y en a qu’un entre 1 et 10, à savoir 6; un entre 10 et 100, à savoir 28; un entre 100 et 1 000, à savoir 496; et un entre 1 000 et 10 000, soit 8 128. Les nombres parfaits sont trouvés par la règle suivante: Le premier nombre de la série de nombres pairs (1, 2, 4, 8, 16, 32, etc.) est ajouté au deuxième nombre de la série, et si il en résulte un nombre incomposite multiplié par le dernier nombre de la série de nombres pairs dont la somme l’a produit. Le produit est le premier nombre parfait.
Par exemple: les premiers et deuxièmes nombres pairs sont 1 et 2. Leur somme est 3, un nombre incomposite.
Si 3 est multiplié par 2, le dernier numéro de la série de nombres pairs-pairs utilisés pour le produire, le produit est 6, le premier nombre parfait. Si l’ajout des nombres pairs ne donne pas un nombre incomposite, le prochain numéro pair de la série doit être ajouté jusqu’à l’obtention d’un nombre incomposite. Le deuxième nombre parfait se présente de la manière suivante: La somme des nombres pairs-égaux 1, 2 et 4 est 7, un nombre incomposite. Si 7 est multiplié par 4 (le dernier de la série des nombres pairs-pairs utilisés pour le produire), le produit est 28, le deuxième nombre parfait. Cette méthode de calcul peut être poursuivie à l’infini. Les nombres parfaits, multipliés par 2, produisent des nombres surabondants, et divisés par 2, des nombres déficients.
Les pythagoriciens ont développé leur philosophie à partir de la science des nombres. La citation suivante de Theoretic Arithmetic est un excellent exemple de cette pratique: « .. Il est évident que les nombres parfaits ont une grande similitude avec les vertus. Mais elles ressemblent aussi aux vertus qui sont rares, car peu nombreuses, et qui sont générées dans un ordre constant. Au contraire, on peut trouver une multitude infinie de nombres surabondants et faibles, pas plus qu’ils ne sont disposés en une série ordonnée, ni générés à partir d’une fin certaine; et par conséquent ils ont une grande similitude avec les vices, qui sont nombreux, démesurés et indéfinis. »
LA TABLE DES DIX NOMBRES
(Le schéma suivant des nombres de Pythagore est une paraphrase des écrits de Nicomaque, de Theon de Smyrne, de Proclus, de Porphyre, de Plutarque, de Clément d’Alexandrie, d’Aristote et d’autres autorités primitives.)
Monade –1 – s’appelle ainsi parce qu’il reste toujours dans le même état, c’est-à-dire séparé de la multitude. Ses attributs sont les suivants: Il s’appelle esprit, parce que l’esprit est stable et a la prééminence; hermaphrodite, parce qu’il est à la fois masculin et féminin; étrange et même, pour être ajouté au même, cela rend étrange, et à l’étranger, même; Dieu, parce que c’est le commencement et la fin de tout, mais que lui-même n’a ni commencement ni fin; bien, telle est la nature de Dieu; le réceptacle de la matière, car il produit la duade, qui est essentiellement matérielle.
La monade pythagoricienne était appelée chaos, obscurité, gouffre, Tartare, Styx, abysse, Léthé, Atlas, Axe, Morpho (un des noms de Vénus), et Tour ou Trône de Jupiter, en raison de la grande puissance qui réside dans le centre de l’univers et contrôle le mouvement circulaire des planètes sur elles-mêmes. La Monade est aussi appelée cause primordiale, car c’est l’origine de toutes les pensées de l’univers. Les autres noms qui lui ont été donnés sont: Apollon, en raison de sa relation avec le soleil; Prométhée, parce qu’il a apporté la lumière à l’homme; Pyralios, celui qui existe dans le feu; génitrice, car sans elle, aucun nombre ne peut exister; substance, parce que la substance est primaire; cause de la vérité; et constitution de la symphonie: tout cela parce qu’elle est primordiale.
Entre le plus grand et le plus petit la monade est égale; entre intention et action elle est le milieu; dans la multitude elle est le centre; et dans le temps elle est le présent, parce que l’éternité ne connaît ni passé ni avenir. Elle est Jupiter, parce qu’il est le père et le chef des dieux; Vesta, le feu de la maison, car elle est située au milieu de l’univers et n’y reste pas inclinée comme un point dans un cercle; forme, parce qu’elle circonscrit, comprend et se termine; l’amour, la concorde et la piété, parce que c’est indivisible. Les autres noms symboliques de la monade sont navire, char, Proteus (un dieu capable de changer de forme), Mnémosyne et Polyonymous (qui a de nombreux noms).
Les noms symboliques suivants ont été attribués à la duade – 2 – car elle a été divisée et correspond à deux plutôt qu’à un; et quand il y en a deux, chacun s’oppose à l’autre: génie, mal, obscurité, inégalité, instabilité, mobilité, audace, courage, contention, matière, dissimilarité, partition entre multitude et monade, défaut, absence de forme, indétermination, harmonie, tolérance, origine, abondance, sommet, Phanes, opinion, erreur, altérité, méfiance, impulsion, mort, mouvement, génération, mutation, division, longitude, augmentation, composition, communion, malheur, sustentation, imposition , mariage, âme et science.
Dans son livre Numbers, W. Wynn Westcott dit à propos de la duade: « on l’appelait Audace, son nombre le plus ancien se séparant du divin; les oracles chaldéens la décrivant comme : l’Adytum du silence nourri par Dieu. »
Comme la monade est le père, la duade est la mère; par conséquent, la duade a certains points communs avec les déesses Isis, Rhéa, Phrygie, Lydia, Dindymene (Cybèle) et Cérès; Erato (une des muses); Diane, parce que la lune est croissant; Dictyna, Vénus, Dioné, Cythère; Junon, car elle est à la fois épouse et sœur de Jupiter; et Maia, la mère de Mercure.
Alors que la monade est le symbole de la sagesse, la duade est le symbole de l’ignorance, car elle contient le sens de la séparation – sens qui est le début de l’ignorance. La duade, cependant, est aussi la mère de la sagesse, car son ignorance – de par sa nature même – engendre invariablement la sagesse.
Les pythagoriciens révéraient la monade mais méprisaient la duade, parce qu’elle était le symbole de la polarité. Par le pouvoir de la duade, les profondeurs ont été créées contrairement aux cieux. La profondeur reflétait les cieux et devenait le symbole de l’illusion, car le dessous n’était que le reflet de ce qui était au-dessus. Le bas s’appelait maya, l’illusion, la mer, le grand vide, et pour le symboliser, les mages de Perse portaient des miroirs. Des querelles sont nées de la duade, et en ramenant la monade entre elles, l’équilibre a été rétabli par le Dieu-Sauveur, qui a pris la forme d’un nombre et a été crucifié entre deux voleurs pour les péchés de l’homme.
La triade – 3 – est le premier nombre réellement impair (la monade n’est pas toujours considérée comme un nombre). C’est le premier équilibre des unités; Par conséquent, Pythagore affirmait qu’Apollon avait donné des oracles sur un trépied et avait conseillé l’offre de libation à trois reprises. Les mots clés des qualités de la triade sont l’amitié, la paix, la justice, la prudence, la piété, la tempérance et la vertu. Les divinités suivantes partagent les principes de la triade: Saturne (souverain du temps), Latone, Cornucopiæ (corne d’abondance), Ophion (le grand serpent), Thétis, Hécate, Polymnia (la muse), Pluton, Triton, gouverneur de la mer, Tritogénie, Achelous, et les visages, les furies et les grâces. Ce nombre s’appelle la sagesse, parce que les hommes organisent le présent, prévoient l’avenir et tirent profit des expériences du passé. C’est une source de sagesse et de compréhension. La triade est le nombre des connaissances – musique, géométrie, et astronomie, la science des célestes et des terrestres. Pythagore enseignait que le cube de ce nombre avait le pouvoir du cercle lunaire.
Le caractère sacré de la triade et de son symbole – le triangle – découle du fait qu’elle se compose de la monade et de la duade. La monade est le symbole du père divin et la duade de la grande mère. La triade constituée de ces deux éléments est donc androgyne et symbolise le fait que Dieu a donné naissance à ses mondes à partir de lui-même, lequel, dans son aspect créateur, est toujours symbolisé par le triangle. La monade qui passait dans la duade était donc capable de devenir le parent de la progéniture, car la duade était le ventre de Meru, dans lequel le monde était incubé et dans lequel il existe toujours sous forme embryonnaire.
Les pythagoriciens estimaient que le tétrade – 4 – constituait le nombre premier né, la racine de toutes choses, la fontaine de la nature et le nombre le plus parfait. Toutes les tétrades sont intellectuelles; elles ont un ordre émergent et encerclent le monde au moment où l’Empyrée (sphère la plus élevée des sphères célestes) le traverse. Pourquoi les pythagoriciens ont exprimé Dieu comme une tétrade est expliqué dans un discours sacré attribué à Pythagore, dans lequel Dieu est appelé le nombre des nombres. En effet, la décade, ou 10, est composée de 1, 2, 3 et 4. Le nombre 4 est symbolique de Dieu car il est symbolique des quatre premiers nombres. De plus, la tétrade est le centre de la semaine, à mi-chemin entre 1 et 7. La tétrade est également le premier solide géométrique.
Pythagore a soutenu que l’âme de l’homme est constituée d’une tétrade, les quatre pouvoirs de l’âme étant l’esprit, la science, l’opinion et le sens. La tétrade relie tous les êtres, éléments, nombres et saisons; rien ne peut être nommé qui ne dépend pas des tetractys. C’est la cause de toutes choses, le Dieu intelligible, auteur du bien céleste et sensible, Plutarque interprète ce tétractisme, qui, dit-il, était aussi appelé le monde, comme étant 36, composé des quatre premiers nombres impairs ajoutés au premier quatre nombres pairs, ainsi:
| 1 + 3 +5 +7 | = 16 |
| 2 + 4 + 6 + 8 | = 20 |
| 36 |
Les mots clés donnés à la tétrade sont: impétuosité, force, virilité, deux fois enfanté et principal gardien de la Nature, car la constitution universelle ne peut être sans elle. C’est ce qu’on appelle l’harmonie et la première profondeur. Les divinités suivantes ont pris part à la nature de la tétrade: Hercule, Mercure, Vulcain, Bacchus et Uranie (une des muses).
La triade représente les couleurs primaires et les planètes principales, tandis que la tétrade représente les couleurs secondaires et les planètes mineures. Du premier triangle sortent les sept esprits, symbolisés par un triangle et un carré. Ceux-ci forment ensemble le tablier maçonnique.
La pentade – 5 – est l’union d’un nombre impair et pair (3 et 2). Chez les Grecs, le pentagramme était le symbole sacré de la lumière, de la santé et de la vitalité. Il symbolisait également le cinquième élément – l’éther – car il est exempt des perturbations des quatre éléments inférieurs. Cela s’appelle l’équilibre, car il divise le nombre parfait 10 en deux parties égales.
La pentade est symbolique de la nature, car, multipliée par elle-même, elle revient en elle-même, tout comme les grains de blé, sous forme de graine, passent par les processus de la nature et reproduisent la graine de blé comme forme ultime de leur propre croissance. Les autres nombres multipliés par eux-mêmes produisent d’autres nombres, mais seuls 5 et 6 multipliés par eux-mêmes représentent et conservent leur nombre d’origine comme dernier chiffre de leurs produits.
La pentade représente tous les êtres supérieurs et inférieurs. Il est parfois appelé l’hiérophante, ou le prêtre des mystères, en raison de sa connexion avec les éthers spirituels, par lesquels le développement mystique est atteint. Les mots clés de la pentade sont réconciliation, alternance, mariage, immortalité, cordialité, providence et son. Parmi les divinités qui ont pris part à la nature de la pentade figuraient Pallas, Némésis, Bubastis (Bast), Vénus, Androgynie, Cythérée et les messagers de Jupiter.
La tétrade (les éléments) plus la monade équivaut à la pentade. Les pythagoriciens ont enseigné que les éléments de la terre, du feu, de l’air et de l’eau étaient imprégnés d’une substance appelée éther, base de la vitalité et de la vie. Par conséquent, ils ont choisi l’étoile à cinq branches, ou le pentagramme, comme symbole de la vitalité, de la santé et de l’interpénétration.
Les philosophes avaient coutume de dissimuler l’élément de la terre sous le symbole d’un dragon, et il a été dit à de nombreux héros de l’Antiquité d’aller de l’avant et de tuer le dragon. Par conséquent, ils ont planté leur épée (la monade) dans le corps du dragon (la tétrade). Cela a abouti à la formation de la pentade, symbole de la victoire de la nature spirituelle sur la nature matérielle. Les quatre éléments sont symbolisés dans les premières écritures bibliques par les quatre rivières sortant du jardin d’Éden. Les éléments eux-mêmes sont sous le contrôle des Chérubins composites d’Ézéchiel.
Les pythagoriciens considéraient l’hexade – 6 – comme représentative, selon la conception de Clément d’Alexandrie, de la création du monde selon les prophètes et les anciens Mystères. Les pythagoriciens l’appelaient la perfection de toutes les parties. Ce nombre était particulièrement sacré pour Orphée, ainsi que pour le destin, Lachesis, et la muse, Thalia. On l’appelait la forme des formes, l’articulation de l’univers et le créateur de l’âme.
Chez les Grecs, l’harmonie et l’âme étaient considérées comme étant de nature similaire, car toutes les âmes sont harmoniques. L’hexade est aussi le symbole du mariage, car il est formé par l’union de deux triangles, l’un masculin et l’autre féminin. Parmi les mots clés donnés à l’hexade, on trouve: Temps, car c’est la mesure de la durée; Panacée, parce que la santé est l’équilibre et que l’hexade est un nombre équilibré; Monde, parce que le monde, comme l’hexade, est souvent considéré comme constitué de contraires par harmonie; auto-suffisant, car ses parties sont suffisantes pour la totalité (3 +2 + 1 = 6); sans fatigue, car il contient les éléments de l’immortalité.
Par les pythagoriciens, l’heptade – 7 – était appelée « digne de vénération ». Elle était considérée comme le nombre des religions, car l’homme est contrôlé par sept esprits célestes à qui il convient de faire des offrandes. On l’appelait le nombre des vies, car on croyait que les créatures humaines nées au septième mois de la vie embryonnaire vivaient habituellement, mais celles nées au huitième mois mouraient souvent. Un auteur l’a appelée la Vierge sans mère, Minerve, parce qu’elle n’était pas née d’une mère mais de la couronne ou de la tête du Père, la monade. Les mots clés de l’heptade sont fortune, occasion, garde, contrôle, gouvernement, jugement, rêves, voix, sons et ce qui mène toutes choses et à leur fin. Les déités dont l’heptade exprimait les attributs étaient Athéna, Osiris, Mars et Clio (une des muses).
Pour de nombreuses nations anciennes, l’heptade est un nombre sacré. Les Elohim des Juifs étaient supposés être au nombre de sept. Il étaient les Esprits de l’Aube, plus communément appelés les Archanges contrôlant les planètes. Les sept Archanges, avec les trois esprits contrôlant le soleil dans son aspect triple, constituent le 10, la décade sacrée de Pythagore. Les mystérieuses tetractys de Pythagore, ou quatre rangées de points, augmentant de 1 à 4, étaient symboliques des étapes de la création. La grande vérité pythagoricienne selon laquelle toutes les choses de la nature sont régénérées par le biais de la décade, ou dix, est subtilement préservée dans la franc-maçonnerie par l’union des dix doigts, cinq sur la main de chaque personne.
Les 3 (esprit, conscience et âme) descendent dans le 4 (le monde), la somme étant le 7 ou la nature mystique de l’homme, consistant en un corps spirituel triple et une forme matérielle quadruple. Celles-ci sont symbolisées par le cube, qui a six surfaces et un septième point mystérieux. Les six surfaces sont les directions: nord, est, sud, ouest, haut et bas; ou avant, arrière, droite, gauche, en haut et en bas; ou encore, terre, feu, air, eau, esprit et matière. Au milieu de ceux-ci se trouve le 1, qui est la figure verticale de l’homme, d’où rayonnent six pyramides au centre du cube. De là provient le grand axiome occulte: « Le centre est le père des directions, des dimensions et des distances. » L’heptade est le numéro de la loi, car c’est le nombre des auteurs de la loi cosmique, les Sept Esprits devant le trône.
L’ogdoade – 8 – était sacrée parce que c’était le numéro du premier cube, dont la forme avait huit angles et était le seul numéro pair-10 (1-2-4-8-4-2-1). Ainsi, le 8 est divisé en deux 4, chaque 4 est divisé en deux 2 et chaque 2 est divisé en deux 1, rétablissant ainsi la monade. Parmi les mots clés de l’ogdoade figurent l’amour, les conseils, la prudence, la loi et la commodité. Panarmonia, Rhéa, Cybèle, Cadmée, Dindymene, Orcia, Neptune, Thémis et Euterpe (une muse) font partie de ses divinités. L’ogdoade était un nombre mystérieux associé aux mystères éleusiniens de la Grèce et des Cabires. On l’appelait le petit nombre sacré. Il tire sa forme en partie des serpents enroulés sur le caducée d’Hermès et en partie du mouvement serpentin des corps célestes; peut-être aussi des nœuds de la lune.
L’ennéade – 9 – était le premier carré d’un nombre impair (3×3). Elle était associée à un échec et à une lacune car elle n’atteignait pas le nombre parfait 10 par un. On l’appelait le numéro d’homme, à cause des neuf mois de sa vie embryonnaire. Parmi ses mots-clés figurent océan et horizon, car pour les anciens, ils étaient illimités. L’ennéade est le nombre illimité parce qu’il n’y a rien au-delà de lui, mais l’infini 10. Il a été appelé frontière et limitation, parce qu’il a rassemblé tous les nombres en lui-même. Il a été appelé la sphère de l’air, car il entoure les nombres comme l’air entoure la terre. Parmi les dieux et déesses qui participaient à chaque degré de sa nature étaient Prométhée, Vulcain, Junon, la sœur et épouse de Jupiter, Pæan et Aglaia, Tritogénie, les Curètes, Proserpine, Hypérion et Terpsichore (une muse). Le 9 était considéré comme diabolique, car c’était un 6 inversé. Selon les Mystères Éleusiniens, c’était le nombre de sphères à travers lesquelles la conscience passait sur le chemin de la naissance. En raison de sa ressemblance avec le spermatozoïde, le 9 a été associé à la vie germinale. Selon les pythagoriciens, la décade est le plus grand nombre, non seulement parce que ce sont les tetractys (les 10 points), mais parce qu’elle comprend toutes les proportions arithmétiques et harmoniques. Pythagore a dit que 10 est la nature du nombre, car toutes les nations y tiennent pour compte et quand elles y arrivent, elles retournent à la monade. La décade s’appelait à la fois le paradis et le monde, car la première incluait la seconde. Étant un nombre parfait, la décade a été appliquée par les pythagoriciens à des choses relatives à l’âge, au pouvoir, à la foi, à la nécessité et au pouvoir de la mémoire. On l’appelait aussi sans fatigue, parce que, comme Dieu, elle était infatigable. Les pythagoriciens ont divisé les corps célestes en dix ordres. Ils ont également enseigné que la décade perfectionnait tous les nombres et comprenait en elle-même la nature d’impair et égal, déplacé et inébranlable, bon et mauvais. Le système décimal peut probablement être retracé à l’époque où il était d’usage de compter sur les doigts, ces derniers étant parmi les plus primitifs des calculateurs et encore utilisés par de nombreux peuples autochtones.

PYTHAGORE, LE PREMIER PHILOSOPHE.
Historia Deorum Fatidicorum.
Pendant sa jeunesse, Pythagore était un disciple de Pherecydes et Hermodamas, et pendant son adolescence il est devenu célèbre pour la clarté de ses concepts philosophiques. De grande taille, il dépassait les 1m82; son corps était aussi harmonieux que celui d’Apollon. Pythagore était la personnification de la majesté et du pouvoir, et en sa présence un sentiment d’humilité et de peur prévalait. En grandissant, sa puissance physique s’est accrue, de sorte qu’en approchant du siècle, il était réellement dans la force de l’âge. L’influence de cette grande âme sur ceux qui l’entouraient était telle qu’un mot de louange de Pythagore remplissait ses disciples d’extase, tandis que l’un d’eux se suicida parce que le Maître s’irrita un jour à propos de quelque chose qu’il possédait. Pythagore fut tellement impressionné par cette tragédie qu’il ne parla plus jamais de qui que ce soit.
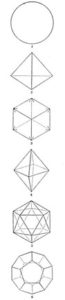
LE SOLIDE GEOMETRIQUE SYMETRIQUE.
Aux cinq solides symétriques des anciens, on ajoute la sphère (1), la plus parfaite de toutes les formes créées. Les cinq solides de Pythagore sont : le tétraèdre (2) avec quatre triangles équilatéraux comme faces; le cube (3) avec six carrés comme faces; l’octaèdre (4) avec huit triangles équilatéraux comme faces; l’icosaèdre (5) avec vingt triangles équilatéraux comme faces; et le dodécaèdre (6) avec douze pentagones réguliers comme faces.
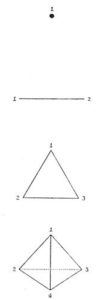
NOMBRES APPARENTES A LA FORME.
Pythagore a enseigné que le point symbolisait le pouvoir du nombre 1, la ligne le pouvoir du nombre 2, la surface la puissance du nombre 3 et le pouvoir du nombre 4.
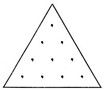
LA TETRAKTYS
Theon de Smyrne déclarait que les dix points, ou tetractys de Pythagore, étaient un symbole de la plus haute importance, car ils révélaient à l’esprit averti le mystère de la nature universelle. Les pythagoriciens se liaient par le serment suivant: ‘Par celui qui a donné à notre âme les tetractys, qui sont la fontaine et la racine de la nature toujours naissante.’
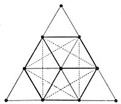
LE CUBE ET L’ETOILE
En reliant les dix points des tetractys, neuf triangles sont formés. Six d’entre eux participent à la formation du cube. Les mêmes triangles, lorsque les lignes sont correctement dessinées entre eux, révèlent également l’étoile à six pointes avec un point au centre. Seulement sept points sont utilisés pour former le cube et l’étoile. Dans la Qabbale, les trois points d’angle inutilisés représentent la nature causale triple et invisible de l’univers, tandis que les sept points impliqués dans le cube et l’étoile sont les Elohim – les Esprits des sept périodes créatives. Le sabbat, ou septième jour, est le point central.
LES VALEURS NUMÉRIQUES DES ALPHABETS HÉBREU, GREC ET SAMARITAIN.
| Colonne | |
| 1 | Noms des lettres hébraïques. |
| 2 | Lettres Samaritaines. |
| 3 | Lettres hébraïques et chaldéennes. |
| 4 | Équivalents numériques des lettres. |
| 5 | Capitale et petites lettres grecques. |
| 6 | Les lettres marquées d’un astérisque sont celles qui ont été importées de Phénicie en Grèce par Cadmos. |
| 7 | Nom des lettres grecques. |
| 8 | Equivalents anglais les plus proches des lettres hébraïque, grecque et samaritaine. |
REMARQUE.
Lorsqu’il est utilisé à la fin d’un mot, le Tau hébreu a la valeur numérique 440, Caph 500, Mem 600, Nun 700, Pe 800, Tzadi 900.
Un alpha en pointillé et un Aleph en pointillé valent 1 000.
Le système peut s’avérer valable, mais il est sans fondement dans l’Antiquité. La disposition des lettres et des chiffres est la suivante:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| UNE | B | C | ré | E | F | g | H | je |
| J | K | L | M | N | O | P | Q | R |
| S | T | U | V | W | X | Y | Z |
Les lettres sous chacun des chiffres ont la valeur du chiffre en haut de la colonne. Ainsi, dans le mot homme, M = 4, A = 1, N = 5: un total de 10. Les valeurs des nombres sont pratiquement les mêmes que celles données par le système de Pythagore.

LE TAMIS D’ERATOSTHÈNE. (Redessiné à partir de Theoretic Arithmetic de Taylor.)
Ce tamis est un dispositif mathématique créé par Eratosthène vers 230 av. J.-C., dans le but de séparer les nombres impairs composites et incomposites. Son utilisation est extrêmement simple une fois que la théorie a été maîtrisée. Tous les nombres impairs sont d’abord rangés dans leur ordre naturel, comme indiqué dans le deuxième panneau à partir du bas, les numéros impairs. On verra alors que chaque troisième nombre (en commençant par 3) est divisible par 3, chaque cinquième nombre (en commençant par 5;) est divisible par 5, chaque septième nombre (en commençant par 7) est divisible par 7, chaque neuvième nombre (commençant par 9) est divisible par 9, chaque onzième chiffre (commençant par 11) est divisible par 11, et ainsi de suite jusqu’à l’infini. Ce système élimine finalement ce que les Pythagoriciens ont appelé les nombres « incomposites », ou ceux qui n’ont pas de diviseur autre qu’eux-mêmes et l’unité. Ceux-ci se trouveront dans le panneau le plus bas, désignés sous le nom de nombres primaire et non composite. Dans son histoire des mathématiques David Eugene Smith affirme qu’Eratosthène était l’un des plus grands érudits d’Alexandrie et fut appelé par ses admirateurs « le deuxième Platon ». Eratosthène a été éduqué à Athènes et est réputé non seulement pour son tamis mais pour avoir calculé, par une méthode très ingénieuse, la circonférence et le diamètre de la terre. Son estimation du diamètre de la terre n’était que de 80 km inférieure au diamètre polaire accepté par les scientifiques modernes.
Cette réussite mathématique d’Ératosthène constitue une preuve indiscutable qu’au troisième siècle avant Jésus-Christ, les Grecs savaient que la terre était sphérique, mais qu’elle pouvait aussi approcher avec une précision étonnante sa taille réelle et sa distance au soleil, à la terre et à la lune. Aristarque de Samos, un autre grand astronome et mathématicien grec, qui vécut environ 250 ans avant notre ère, établi par déduction philosophique et quelques instruments scientifiques simples que la terre tournait autour du soleil. Alors que Copernic se pensait réellement le découvreur de ce fait, il a toutefois rappelé les conclusions avancées par Aristarque dix-sept cent ans plus tôt.

