Introduction
Les civilisations préhistoriques possédaient des connaissances mathématiques étonnantes, généralement accompagnées et animées d’une préoccupation maniaque de la mesure du temps et de l’étude des objets visibles dans le ciel. Dans certains cas, ces calendriers historiques mesuraient les longueurs de l’année et du mois avec une précision qui n’a été atteinte qu’au XIXe siècle. Il n’y a aucun moyen de conclure qu’une civilisation avec des connaissances exceptionnelles a été perdue dans une période intérimaire. Globalement congruents – ou du moins très similaires dans leur contenu – les mythes détaillent l’effondrement d’une telle civilisation. En conséquence, ce n’était pas tant la conséquence des guerres, mais les hautes cultures ont péri à la suite d’une catastrophe environnementale.
Résumé historique
Une grande partie de ce qui a été redécouvert au cours de la Renaissance avait auparavant été perdu du canon conscient de la connaissance en un laps de temps alarmant. Au-delà de la perte connue, nous pouvons difficilement imaginer ce qui avait irrémédiablement disparu. La perte a dû être immense. Nous savons avec certitude qu’en quelques centaines d’années, le Vieux Monde a réussi à perdre complètement le niveau d’éducation et de connaissances atteint par les civilisations anciennes et est retombé au niveau d’un « univers » plein de magie et de superstition. Sans les monastères, les Byzantins et les Arabes préservant le savoir, la perte du savoir aurait été plus importante et probablement définitive. Ainsi, seul un peu a été sauvé et surtout par simple chance. Berose (contemporain d’Alexandre le Grand) affirme qu’à son époque, à Babylone, des rapports remontant à 150 000 ans étaient encore conservés. Cette échelle de temps contredit toutes les datations de l’histoire ancienne officielle. Sur Berose et son œuvre, nous en savons peu. Des fragments de ses livres ne sont conservés que dans des citations, principalement dans les écrits d’Eusèbe de Césarée (500 ans plus tard). D’autres écrivains de l’ère préchrétienne ont rapporté que les archives égyptiennes remontaient également à un passé similaire.
Ce n’est pas seulement en Mésopotamie et en Égypte, où l’on retrouve les vestiges de connaissances perdues, la situation dans d’autres endroits semble tout aussi désastreuse. On sait par exemple que l’empereur chinois Tsin-chi-hoang-ti (246-209 avant JC) excellait dans la destruction des savoirs anciens. Il a non seulement construit la Grande Muraille de Chine, mais a également laissé brûler tous les livres anciens, à l’exception de ceux de la médecine et des enseignements moraux.
Cultures anciennes
Quand on parle d’antiquité, on se réfère généralement à des civilisations qui ne remontent pas à plus de 3500 avant JC au maximum. Étonnamment, les hautes cultures sont apparues simultanément dans des régions éloignées. Cette coïncidence temporelle de la floraison de ces – pour nous – « nouvelles » civilisations historiques après le premier âge des ténèbres préhistorique va au-delà de la coïncidence. Pour beaucoup, ce réveil de la contemporanéité des civilisations anciennes dans différentes régions suggère une puissance mondiale agissant en arrière-plan.
Pour devenir concret dans cette évaluation, le 13 août 3114 avant JC est l’heure zéro du calendrier maya. Ce jour-là, leur célèbre Compte Long de leur nouvelle ère a commencé. À peine différent du calendrier maya, le livre indien « Surya Siddhanta » désigne l’heure zéro à minuit du 17 au 18 février 3102 av. Cette nuit-là, pour les hindous, l’âge actuel du Kali-Yuga a commencé. Selon la contribution de CW Beyer dans le livre de SJ Baumgarten, le début du calendrier égyptien tombe le 22 mars de l’année 3069 avant JC, ce qui est proche des deux dates ci-dessus.
De plus, des parallèles incroyables peuvent être établis entre le début du calendrier maya et l’émergence de calendriers dans d’autres régions du monde antique dont les gens ont également choisi ce siècle comme début de leur époque. Les mythes perses et chinois rapportent que quatre étoiles brillantes ont agi en tant que gardiennes des quatre directions particulières (équinoxe et solstice) dans le ciel nocturne. Si nous supposons le lever du soleil à la date des équinoxes et des solstices comme le temps, nous détectons un accord remarquable. Il y a 5 000 ans, quatre étoiles de la 1ère magnitude (Aldebaran, Antares, Regulus et Fomalhaut) ont été vues dans le ciel du matin de telle manière qu’elles pourraient être considérées agir en tant que gardien du lever du soleil.

Gauche : La pierre solaire aztèque (ou pierre calendaire) représentant les cinq mondes consécutifs.
‘Aztekenkalender’ par Anagoria ( CCBY3.0 )
À droite : Explication illustrative de la façon dont les deux calendriers mayas (Haab – 365 jours – et Tzolkin – 260 jours –), utilisés en parallèle, étaient organisés à Baktun, Katun, Ahau et Tun suivis de Winal et K’in, où 1 K’ dans correspond à 1 jour. Montré également comment Haab et Tzolkin se rapportent.
‘El Baktun en la Cuenta Larga’ par Navelegante ( CCBYSA4.0 )
Non seulement la concordance étroite de la date à laquelle les calendriers ont commencé à intéresser l’historien, mais aussi leur exactitude incroyable transmet un message clair sur les connaissances scientifiques et mathématiques possédées à cette époque. Le calendrier maya surpasse même la précision du calendrier grégorien en usage aujourd’hui. Non seulement le calendrier maya a mesuré la durée de l’orbite de la Terre autour du soleil avec plus de précision que notre calendrier actuel, mais les Mayas ont donné une valeur encore plus précise pour la durée moyenne de l’orbite de la Lune autour de la Terre. La précision atteinte est d’autant plus remarquable que la Lune dans les déserts ou les régions au ciel dégagé a pu jouer un rôle important dans la vie quotidienne en tant que source de lumière nocturne. Mais à quoi sert sa lumière terne dans la forêt tropicale ou les régions nuageuses du monde ?
Par rapport à la valeur la plus exacte d’aujourd’hui de la durée d’un mois (29,5305883 jours), les Mayas ont attribué une période de 29,5302 jours au mois lunaire synodique, qui est 0,0013% plus court que la valeur actuelle la plus précise d’aujourd’hui. Aussi précise que puisse paraître cette valeur, en fait, elle était encore plus précise. Comme la distance entre la Lune et la Terre augmente de 3,8 cm chaque année, la période orbitale augmente de 9,4 s en 100 ans. Compte tenu de la durée d’un mois lunaire maya (source Codex Dresde) à 357 ans, la distance était de 13,6 m plus étroite qu’aujourd’hui. A cette époque, la valeur maya était sans aucun écart par rapport à la meilleure valeur moderne. La précision atteinte est également incroyable car la durée de l’orbite de la Lune est soumise à de nombreuses fluctuations. La lunaison – déterminant la variation de la durée d’une orbite lunaire – est l’un des calculs de mécanique céleste les plus difficiles. Sans support par des calculs mathématiques, des siècles d’observations sont nécessaires pour faire la moyenne de ces fluctuations et atteindre la précision ci-dessus. Les Mayas (et leurs cultures antérieures) auraient procédé de cette manière. Ah bon?
Encore une fois, comment exactement le temps mesuré par les Mayas illustre leur valeur pour la durée de l’année. L’écart par rapport à la meilleure valeur actuelle (365,24219878173 jours) se produit au 7e chiffre. Est-ce encore inexact ou la valeur 365,242… effectivement utilisée a-t-elle été délibérément interrompue ? La bonne raison existe. En fait, une précision accrue devient absurde lorsqu’il faut attendre plusieurs milliers d’années avant qu’un jour intercalaire ne soit inséré ou omis. La différence de valeurs numériques entre le calendrier maya et la valeur actuelle la plus connue – non relative au calendrier actuellement utilisé – est de 0,002 %. L’erreur de 26 secondes, par laquelle le calendrier grégorien indique l’année trop longue, est réduite dans le calendrier maya à 7 secondes trop courte.
Parler d’erreur est également trompeur car la Terre ralentit dans sa rotation en raison du frottement des marées. Dans la précision, la gamme citée l’allongement de la période de 0,0016 s par siècle ne doit plus être négligé. Il y a 4 500 ans, aucun écart n’existait entre la durée exacte de l’année et l’ancienne valeur maya. Le calendrier maya était alors – dans le cadre de la précision de mesure d’aujourd’hui – exact. S’il avait été réellement introduit en 3100 av.
Comment était-il possible pour un peuple qui technologiquement avait à peine dépassé l’âge néolithique de déterminer la longueur de l’année au millionième de millionième ? Dans la littérature, une solution circule, qui permettrait prétendument cette précision en utilisant la méthode de mesure la plus simple. La solution et un défi – prétendument gérable – restant réside dans une période de mesure suffisamment longue.
Les Mayas – et leurs prédécesseurs – ont en fait érigé des bâtiments qui fonctionnaient comme des chronomètres. Ce n’est qu’à une certaine heure d’un seul jour de l’année que la lumière du soleil traversait une fissure ou une allée. Si les jours entre deux événements uniques étaient comptés correctement, un raffinement constant était obtenu au fil du temps. Selon cette explication, bien que le résultat semble sophistiqué, il a été déterminé par une simple force brute.

Un « chronomètre » maya dans les ruines de Dzibilchaltun (Temple des Poupées)
Aux équinoxes de printemps et d’automne, le soleil levant brille à travers la porte du temple.
‘Dzibilchaltún Maya Ruins’ par Larry Syverson ( CCBYSA2.0 )
Jusqu’ici, facile ? Plutôt pas. Selon cette théorie, les Mayas devaient enregistrer et tenir leurs livres impeccablement pendant toute la période de comptage. Après avoir terminé le décompte, ils ont ajusté leur calendrier d’une manière très complexe. Apparemment, ils se sont entièrement appuyés sur des nombres entiers, leur calendrier inséré 13 jours tous les 52 ans et soustrait 25 jours tous les 3 172 ans. Puisque leur calendrier commence en l’an 3114 av. Cependant, cette explication du long comptage considéré comme la solution au problème propagé par l’archéologie présente un inconvénient majeur. Quelle civilisation conserve des archives pendant 3 000 ans avec une telle précision ? Transféré à notre époque. Si nous voulons établir un calendrier par cette méthode, déjà les pharaons avaient dû commencer à compter et depuis lors, pas un seul jour ne s’est glissé par erreur. L’ampleur de ce défi devient évidente si l’on considère que les premiers chrétiens n’étaient même pas capables de déterminer correctement l’année de la naissance du Christ. Sans parler du jour. Et cet événement a dû être retracé uniquement sur quelques siècles plutôt que sur quelques millénaires.
Quiconque croit en cette théorie du comptage à long terme est au moins un optimiste. L’idée d’un long comptage, où à un moment donné un chaman a commencé à enregistrer les jours et les mois comme une feuille de pointage sur une feuille de palmier afin d’en développer un calendrier compliqué, n’est même plus absurde, c’est juste ridicule.
Pourquoi les Mayas ont incorporé la période orbitale de Vénus dans leur calendrier est encore un autre mystère.
Les Mayas ont déterminé que l’année de Vénus comprend 584 jours. L’écart restant par rapport à la valeur exacte de 583,92 jours ne résulte probablement pas d’une erreur de mesure, mais était dû à la nécessité d’établir une connexion avec les deux autres calendriers utilisés (le calendrier rituel de 260 jours et le calendrier solaire de 365 jours plus les correctifs). Étant donné que le rapport des temps orbitaux de Vénus à la Terre est proche, mais pas exactement de 13 : 8 et donc non commensurable, les mathématiciens de l’âge de pierre n’ont eu d’autre choix que de dissimuler le dilemme de l’adaptation au moyen de l’imprécision.
Les Mayas ont poussé le culte du calendrier à ses extrêmes. Cependant, ils n’étaient pas les seuls à s’efforcer d’obtenir une précision étrange en matière de calendrier. Dans le Surya Siromani indien, la durée d’une année sidérale comprend 365 jours, 6 heures, 12 minutes et 9 secondes. En notation décimale, cela correspond à la longueur de l’année qui est de 365,258438 jours. Par rapport à la valeur réelle, c’est 23,4 minutes de trop. Cette erreur est beaucoup trop importante compte tenu des chiffres indiqués et contredit la précision avec laquelle les constellations et les positions des étoiles ont été calculées. Si l’on ose corriger une éventuelle erreur de signe et utiliser moins 12 minutes au lieu de plus 12 minutes dans son calcul, ce changement de signe réduit l’écart par rapport à la valeur vraie à 37 secondes.
Dans un autre livre indien classique sur l’astronomie préhistorique, le Surya Siddhanta, l’année comprend 365 jours, 6 heures, 12 minutes et 36,56 secondes. Cette spécification devient exacte lorsque nous supposons à nouveau la même erreur de signe. Ce faisant, cette correction de signe certes audacieuse réduit l’écart par rapport à la meilleure valeur actuelle à 9,4 secondes par rapport à la valeur exacte.
Malgré quelques doutes, les corrections proposées semblent justifiées, d’autant plus que ces deux livres indiens montrent à plusieurs reprises des incohérences dans les schémas et les explications. Nous pouvons supposer que des livres plus anciens et maintenant perdus ont été révisés lors de la compilation par les copistes en recueils simplifiant les problèmes. Très probablement, les auteurs de Surya Siddhanta ont consulté et copié des extraits de sources de qualité variable et n’ont compris que partiellement les détails des originaux. Des erreurs se sont glissées lors de la copie ou de la reprise d’extraits. On a même l’impression qu’ils ont corrigé les erreurs suspectées pour les adapter à leur propre compréhension lorsque les problèmes sont devenus trop complexes et incompréhensibles. Parfois, cela semble être un manque de diligence. Cette méconnaissance fondamentale ou insouciance se manifeste dans le cas de confusions évidentes. Le Surya Siddhanta cite la durée du jour sidéral à 86 400 secondes, bien que ce soit la durée du jour synodique. Une erreur qu’aucun professionnel n’aurait commise et qui s’explique mieux par l’imprudence.
Parfois, les connaissances perdues ne deviennent reconnaissables qu’à la deuxième vue. Sans mentionner un arrière-plan de calendrier, Abydenos dit dans ses ‘Chroniques de l’ancienne Egypte’, manuscrit sauvegardé en partie seulement, que 30 dynasties ont régné sur l’Égypte pendant 36 525 ans. La séquence de chiffres n’est certainement pas une coïncidence. Car dans ce nombre, tous les chiffres du nombre de jours du calendrier julien sont reproduits. Bien que du vivant d’Abydenos, le calendrier julien ait été en usage, reproduire cette chaîne est néanmoins extrêmement étonnant. Ce qui nous semble être une représentation triviale de chiffres était étranger aux peuples des anciennes cultures égyptienne et européenne. Les Grecs et les Romains ne savaient pas comment écrire les nombres en notation décimale, car c’était tout simplement impossible avec leur système de numération. Dans tous les cas, en raison de la notation utilisée, la représentation des valeurs non entières sous forme de décimales était inconnue.
En fait, l’utilisation des fractions décimales n’a été introduite qu’au XVIIe siècle. Ainsi, et peut-être de manière surprenante, à y regarder de plus près, même les nouvelles les plus simples deviennent inexplicables.
Mathématiques
La qualité différente des sources consultées par les deux anciens recueils indiens et la révision incorrecte de la copie sont également illustrées de manière frappante par les données concernant le nombre Pi. Les données sur la relation entre le diamètre et la circonférence de la Terre suggèrent que les premiers auteurs connaissaient le nombre Pi à au moins cinq chiffres décimaux. Le Surya Siddhanta ainsi que le Surya Siromani mesurent les longueurs en unités de yojana. Si l’unité de longueur originale a été conservée au fil du temps jusqu’à aujourd’hui, alors 1 yojana équivaut à 14,56 km. Dans le Surya Siromani, le diamètre de la Terre est de 1 581 (1/24) yojanas et la circonférence de la Terre de 4 967 yojanas. Calculé sur la base de ces deux chiffres, Pi vaut 3,141599684…, qui est en fait remarquablement proche des premiers chiffres de Pi (3,141592654…). Remarque : peu importe à quel point nous connaissons la longueur réelle d’un yojana, cela ne change pas les chiffres de Pi.
Les anciens Indiens ne connaissaient pas seulement la valeur de Pi, ils connaissaient évidemment aussi la formule pour calculer la surface d’une sphère à partir du rayon :
![]()
Le rapport déclaré de la circonférence et du diamètre de la Terre suggère une connaissance incroyablement précise de la valeur de Pi. Cette précision n’était pas le fruit du hasard. La même précision pour Pi découle des données sur la surface de la Terre, qui sont données sous la forme de 7 853 034 yojanas carrés. Le calcul à rebours de Pi à partir de l’indication de surface et du diamètre de la Terre s’écarte de 2 millionièmes (écart au 6e chiffre) de la vraie valeur de Pi.

Visualisation de l’approche 4 d’Archimède pour déterminer Pi (La longueur de la base des petits triangles
est ajoutée et liée au rayon.)
« Aire d’un cercle » par Sven ( CCBYSA3.0 )
La formule pour calculer la surface d’une sphère était probablement déjà connue des Égyptiens. Tant les Indiens que les Égyptiens avaient plusieurs milliers d’années d’avance sur le découvreur officiellement répertorié de la formule, le savant grec Archimède. Il a imbriqué Pi dans l’intervalle entre supérieur à 3 + 10/71 et inférieur à 3 + 10/70. Ainsi, il a estimé que la valeur de Pi était 3,1428571, ce qui est environ 100 fois moins précis que la valeur donnée dans l’Inde ancienne.
Terre et espace
Les livres Surya Siddhanta et Siddhanta-Siromani impressionnent non seulement par leurs connaissances mathématiques et – dans une certaine mesure – par des informations précises sur la taille de la Terre, mais aussi par l’établissement de données géophysiques et astronomiques quantitatives supplémentaires. Dans le Siddhanta-Siromani, la hauteur de l’atmosphère terrestre est spécifiée à 175 km. C’est deux fois la hauteur de la stratification que nous appelons la stratosphère. À cette altitude, des étoiles filantes commencent à briller, des ondes radio sont réfléchies et des aurores boréales apparaissent. En contradiction extraordinaire avec l’affirmation de la hauteur limitée de l’atmosphère, Siddhanta-Siromani déclare qu’au-dessus de l’atmosphère soufflent des vents qui poussent les planètes. Le concept de supposer des vents pour le mouvement est l’une des incohérences incompréhensibles et correspond au mélange déroutant d’idées justes et fausses.
La connaissance des Indiens sur le système solaire était assez correcte, car la distance des planètes était estimée au bon ordre de grandeur. Incroyablement, cependant, ils se trompent complètement sur la distance de la Lune à la Terre. Pour cette distance, le Surya Siddhanta indique 324.000 yojana. Ce chiffre correspond à 4 720 000 km et surestime ainsi la distance lunaire moyenne de plus de dix fois. La raison de cette surestimation provient probablement du mauvais modèle de vent comme moteur du mouvement de la planète, puisque les auteurs ont supposé que le vent, qui était à la fois responsable de la poussée des planètes et de la Lune, soufflait à n’importe quelle distance à la même vitesse. De cette hypothèse surgit un dilemme insoluble. Au moins tant que cette théorie du vent est appliquée,
Avec la distance lunaire mal estimée et les vents soufflant uniformément comme base, les anciens Indiens ont calculé la distance entre les planètes (et le Soleil) dans un modèle géocentrique à partir du rapport des temps orbitaux :

En utilisant la période orbitale lunaire de la Lune égale à 27,322 jours comme base, la formule conduit aux données du diagramme 1.
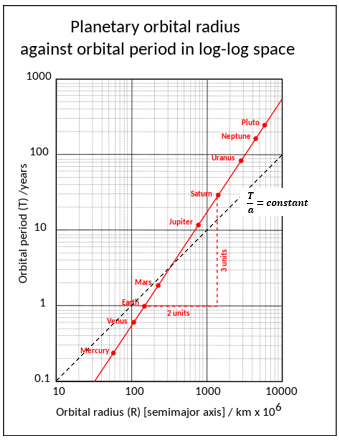
3e loi de Kepler détectable à partir du tracé logarithmique des distances planétaires et de leurs
périodes orbitales.5 La ligne brisée indique la dépendance linéaire si T ~ a.
« Rayons et période du système solaire » par Martinvl ( CCBYSA4.0 )
Ce problème insoluble se pose parce que les périodes réelles des temps de cycle orbital sont proportionnelles à :
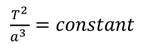
(3. Loi de Kepler) et non comme les Indiens le supposaient :
![]()
T est égal à la période orbitale et le paramètre ‘a’ est le demi-axe principal de l’ellipse orbitale. Pour expliquer l’erreur extraordinaire dans l’indication de la distance de la Lune, on ne peut que supposer qu’un copiste impuissant a compris le sujet et a essayé de sauver l’impossible.
Bien que les valeurs données soient systématiquement fausses selon le facteur de Kepler, elles sont du bon ordre de grandeur. Pour Jupiter, la valeur de distance de Surya Siddhanta s’accorde même assez bien avec la vraie distance. La distance indiquée pour Mercure est trop petite d’un facteur 3, tandis que pour Saturne, elle est 30 % trop grande. En raison de la mauvaise formule utilisée, les distances sont systématiquement erronées, mais dans le modèle utilisé, les calculs sont étonnamment exacts.
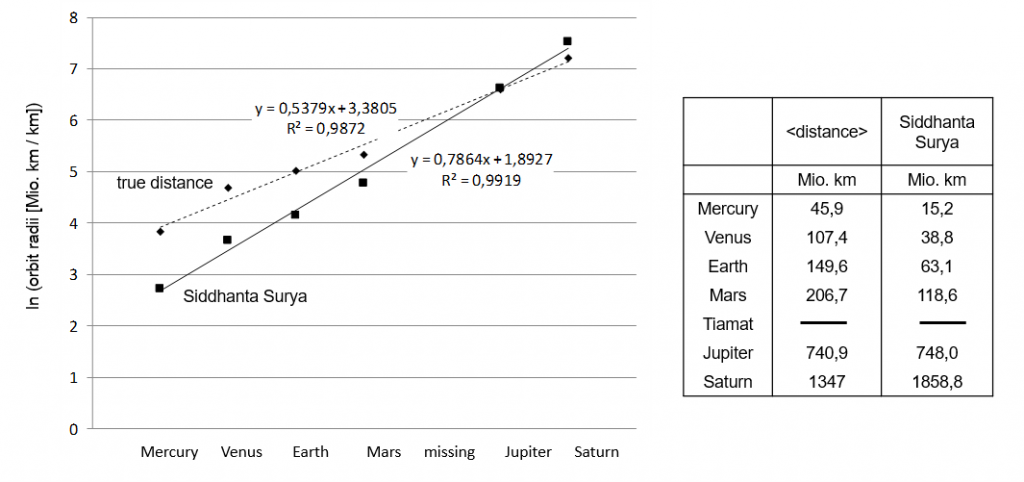
Tracé des distances des planètes comme indiqué dans l’ancienne source indienne par rapport aux valeurs réelles.
La précision au millième des distances des planètes calculées de manière incorrecte mais cohérente par rapport au Soleil s’applique à toutes les planètes, à l’exception de Vénus. Sa distance est citée de 1,3 % trop petite, s’écartant nettement de la formule de calcul. Mais, Vénus, comme nous le montrerons dans un article ultérieur, est de toute façon un cas spécial.
Comme le montrent déjà les valeurs des rayons orbitaux des planètes, les anciens Indiens n’avaient pas peur des grands nombres. Les distances planétaires n’étaient en aucun cas la limite supérieure de leur imagination. Dans le Siddhanta Siromani, le rayon de la région solaire environnante est spécifié à 18 712 080 864 000 000 yojana (~ 28 000 années-lumière). Une valeur appropriée pour notre galaxie, qui mesure 100 000 années-lumière de diamètre et en moyenne 10 000 années-lumière d’épaisseur. Ainsi, le rayon moyen (= région) est déterminé à 30 000 années-lumière dans ce que les Indiens appelaient le voisinage solaire. Même le début du vingtième siècle ne connaissait aucune valeur pour la taille de ce « quartier » étendu.
En outre, d’autres données fournies sont d’un ordre de grandeur correspondant et correct. L’existence du monde est citée dans le Surya Siddhanta à 4.300.560.000 ans. Étonnamment – ou peut-être pas – cette valeur correspond assez étroitement à l’âge de la Terre (valeur estimée aujourd’hui : 4,5 milliards d’années). Selon la croyance hindouiste, 4,32 milliards d’années correspondent à un jour dans la vie de Brahma. Un autre exemple de la façon dont la religion et l’astronomie sont imbriquées ?
Ces chiffres géants sont étonnants si l’on considère que les premiers exégètes bibliques supposaient que la création du monde remonte à 7 000 ans. Pour respecter davantage la valeur de la contribution des anciens Indiens dans ce domaine, il est intéressant de noter qu’un physicien de premier plan du 19ème siècle, Lord Kelvin, a estimé l’âge de la Terre à environ 24 millions d’années maximum.
Ces deux livres représentent une preuve convaincante de la connaissance perdue. Les données correctes sur la Terre, sur les distances astronomiques et le chiffre concernant l’âge de la Terre, sont trop précises et sont loin de la connaissance possible d’une culture de l’âge de pierre pour avoir été accidentellement estimée ou devinée correctement.
Les deux livres anciens ont probablement été écrits il y a environ 3000 ans. Le temps d’origine peut être réduit car le Siddhanta Surya place l’équinoxe vernal dans la constellation du Bélier, de sorte que son origine peut être datée d’environ 1000 av. L’époque du Bélier comprend environ 2000 avant JC jusqu’au début de notre ère.
Ce n’est pas seulement dans l’Amérique ancienne et l’Inde que nous trouvons des connaissances préhistoriques étonnamment sophistiquées, mais aussi en Mésopotamie des rapports correspondants ont été transmis. Comme on peut le voir à partir des enregistrements trouvés dans la bibliothèque du roi assyrien Assurbanipal (668-627 BC), le système énumérative de calcul était basé sur le nombre 12960000. Le même système se trouve sur les plaques de la ville antique sumérienne Nippour et la colonie babylonienne de Sippar. S’agit-il vraiment d’une coïncidence lorsque 2 x 12 960 années correspondent à une année platonique (une rotation de 360° de l’axe de la Terre contre le ciel étoilé) ? Si le choix de cette unité de base n’était pas un hasard, Sumériens et Babyloniens connaissaient déjà la précession de l’axe terrestre avec une précision remarquable.
Les frontières entre l’ésotérisme et les faits s’estompent lorsque des liens sont établis entre les bâtiments préhistoriques et l’échelle de la Lune et de la Terre et d’autres données astronomiques. La pyramide de Khéops et les dimensions de Stonehenge peuvent être interprétées comme étant liées au diamètre de la Terre et de la Lune ou même à la distance au Soleil. Les relations supposées peuvent être surprenantes, mais elles ne sont pas tout à fait appropriées comme preuve de connaissances préhistoriques.
Avec un peu de bonne volonté, des données codées de manière sophistiquée du système planétaire peuvent être dérivées des dimensions et des masses des trois pyramides. Les relations construites de manière absurde ne conduisent en aucun cas à des écarts proches de zéro. Par exemple, la relation des volumes :

tient à < 0,1%. L’écart est dans l’erreur avec laquelle les volumes des pyramides sont connus. Attribuer tout cela à une coïncidence pousse ce contre-argument galvaudé à ses limites. Si ce n’est pas une coïncidence, alors le système planétaire et ses objets étaient bien connus des anciens.
Un peu plus discutable, outre les masses, les diamètres et les orbites planétaires, alors que même les nombres naturels fondamentaux, tels que la vitesse de la lumière, sont dérivés de relations trouvées :
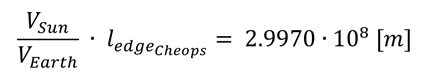
Pour appeler ce nombre, la vitesse de la lumière nécessite une définition identique de l’unité seconde – étant donné que depuis des temps immémoriaux, la division pratiquée de la journée en 24 heures puis la subdivision supplémentaire en soixantièmes d’unités, cela peut être limite mais pas impossible . L’écart par rapport au nombre réel n’est que de 0,03 %. Compte tenu de l’incertitude dans les données de la pyramide, cela se situe à nouveau dans l’erreur de mesure. En tout cas, la simplicité pour obtenir ce résultat est surprenante.
La connaissance des anciennes civilisations avancées classiques – telles que les Mayas, les Sumer, les Indiens et les Égyptiens – est partiellement préservée par écrit. De telles preuves manquent pour l’Europe mégalithique, dont la culture remonte à 6 000 av. Si nous ne comprenons pas les moyens par lesquels les pierres géantes (menhirs) ont été déplacées vers leurs sites, nous sommes également surpris par les connaissances mathématiques approfondies qui ont été appliquées à la construction de ces structures préhistoriques. Par exemple, les rapports d’aspect rationnels des triangles rectangles peuvent être trouvés à la fois dans les grands sertissages en pierre et dans les petites sculptures. Comme A. Thom explique, les premiers peuples d’ Europe du Nord savaient Pythagore théorème non seulement dans le très connu et simplement rationnelle 3, 4, 5 rapport:
3 2 + 4 2 = 5 2
mais aussi, dans des relations moins évidentes telles que 5, 12, 13 et même 12, 35, 37. Alexander Thom et d’autres considèrent les cercles de pierres et les rues marquées de pierres comme des observatoires, qui au moins dans certains cas ont servi à la prédiction de flux et reflux. Quoi qu’il en soit, cela reste un mystère comment l’âge de pierre en est venu à une telle connaissance, et pourquoi et quand il a été perdu.
Le grec ancien
En passant de la préhistoire à l’antiquité, nous devons affirmer que les Grecs avaient une compréhension raisonnablement correcte de la structure du système planétaire bien avant Kepler et Copernic. Non seulement Démocrite a déduit l’existence des atomes par une simple logique, mais aussi l’infinité de l’univers. Il a deviné à juste titre que la Voie lactée représente une collection d’étoiles. Hipparque a conclu que la longueur différente des saisons provenait de la forme elliptique de l’orbite de la Terre. Au moyen de mesures, les Grecs, qui ont d’abord copié les Babyloniens, ont développé une vague idée de la distance de la Lune et du Soleil à la Terre. Approche d’Aristarque, pour déterminer la relation des distances à partir de la position de la Lune en quadrature, reprend essentiellement la méthode d’Eratosthène qui a déterminé la circonférence du globe en comparant l’ombrage à Syène et à Alexandrie. Cette approche représente un chef-d’œuvre intellectuel qui allie ingénieusement géométrie et astronomie. Du mouvement manquant des étoiles pendant l’orbite de la Terre autour du Soleil, Aristarque a conclu correctement en supposant une vision du monde héliocentrique que l’orbite de la Terre doit être minuscule par rapport à la distance des étoiles. Dans leur modèle astronomique, les Grecs avaient 2000 ans d’avance sur Copernic. On sait peu que Copernic connaissait certaines de ces thèses des savants antiques. Était-il un peu plagiaire ? En effet, être le premier n’est pas facile.
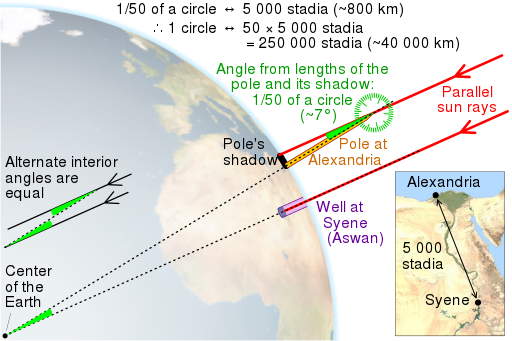
Explication graphique de la méthode utilisée par Ératosthène pour mesurer la circonférence de la Terre
« Eratosthène mesure la circonférence de la Terre » par cmglee, David Monniaux ( CCBYSA4.0 )
Sans aucun doute, les Grecs s’appuyaient sur l’astronomie des Chaldéens. Mais ces maîtres des Grecs utilisaient une description purement algébrique, plutôt que géométrique, des mouvements planétaires. La théorie planétaire des Kidinnu (astronome babylonien ayant vécu vers 400 avant JC) n’est conservée que par fragments, mais ils suffisent à étonner. La précision de ses tables et de ses calculs n’a été retrouvée qu’au XIXe siècle.
Conclusion
Notre compilation de connaissances anciennes est plus qu’incomplète et pourtant, la preuve est que l’histoire officiellement enseignée de l’histoire ancienne brosse non seulement un tableau incomplet, mais est en grande partie simplement une idée fausse. Une lacune fatale, car aussi faibles que soient les indices, ils suffisent à remettre en cause la vision du monde savante.
Alternativement, on pourrait soutenir qu’il y a eu un effondrement de la culture humaine à cause d’un événement désastreux, où peut-être que les connaissances perdues n’étaient pas d’origine indigène mais ont diminué avec la disparition des enseignants, qui étaient considérés comme des extraterrestres.
En fait, dans l’histoire savante, l’existence d’une culture préhistorique perdue est complètement cachée et même pas abordée comme une option. Le fait est que, peu importe nos efforts, ce qui a été complètement effacé et perdu, aucun historien ne peut le reconstituer. D’un autre côté, savoir déjà que l’humanité est autrefois retombée des hauteurs culturelles dans la barbarie profonde est à la fois instructif et un avertissement. Peut-être qu’il n’y a pas de remède comme l’a déjà noté Cicéron, les conflagrations mondiales qui effacent la civilisation n’ont rien d’extraordinaire, mais font partie de notre existence.
Aloys Eiling
Source : https://grahamhancock.com/eilinga3/
